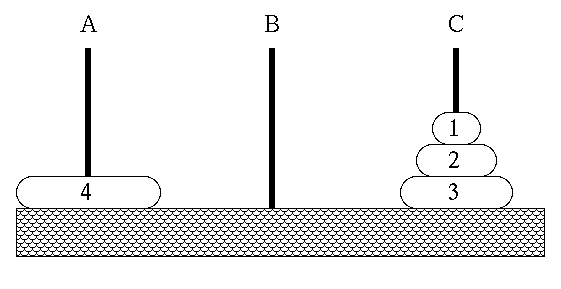
ハノイの塔の問題に戻ろう。
一見難しそうなハノイの塔も、再帰的手法を用いて 問題を分割すると簡単になる。
まず初期状態を見る。
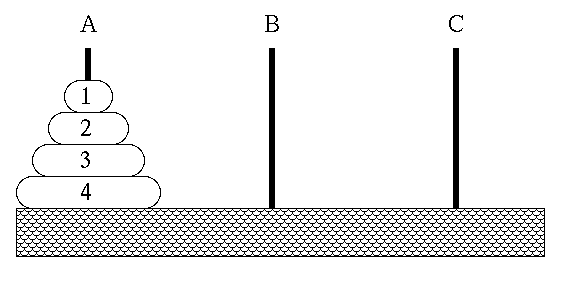
Aに積み重なっている4つの円盤群を、規則に従い1枚ずつBに移したい。 このときに、
「もし私の知らないところで誰かが1から3をAからCに移動してくれれ ば楽だなあ。そしたら私は4番をBに移して、最後にその人に1から3をBに戻しても らえばおしまいだ」
という風に考える。つまり、ハノイの塔に慣れた人を連れて来て、 1から3をCに移動してもらう(下図)。

次に自分で、4をBに移動する(下図)。
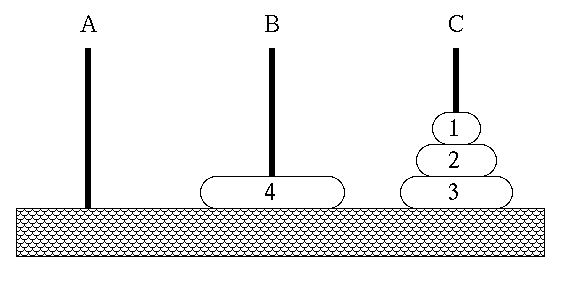
そして、もう一度達人を連れて来て1から3をBに移動してもらう。
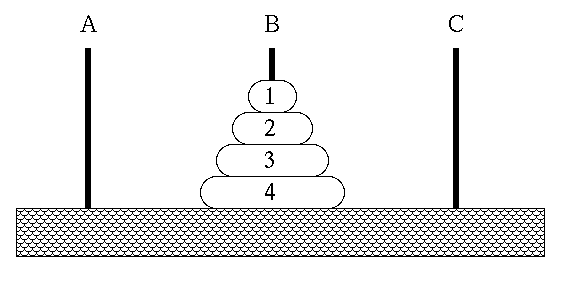
こんなムシのいい考え方でよいのだろうか。よいのである。 連れて来られた達人は次のように考える。
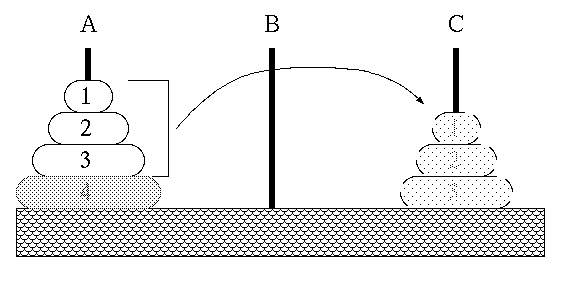
「1から3をAからCに動かせばいいのか。うーむ。 寝てる間に誰かが1から2をAからBに移動してくれれば楽だなあ。 そしたら私は3番をCに移して、最後にその人に1から2をCに 戻してもらえばおしまいだ」
このようにして、
を繰り返していくと、最終的に
となり、最後に頼まれた人は1枚だけ移動すればよくなり、 何も考えなくても移動できることになる。
上記の考え方をRubyメソッドにしよう。
を受け取り、移動手順を解くメソッド hanoi
を考える。
重要な部分をことばで書くと次のようになる。
# n = 枚数
# from = 元の棒の名前
# to = ゴールの棒の名前
# work = 一時的に利用してよい棒の名前
def hanoi(n, from, to, work)
if 1枚か?
「n番の円盤を from から to に移動しなさい」
と表示する(かんたん)
else # 2枚以上の場合
まず n-1 だけを誰かに頼んで、一時待避棒に動かしてもらう
そして「n番の円盤を from から to に移動しなさい」と表示
最後に n-1 を誰かに頼んで、一時待避棒から目的棒に動かしてもらう
end
end
これを実際にRubyプログラムに直すと完成する。