t検定

t検定

何かの平均を求めて全体の傾向を見る調査はしばしば行なわれる。 あるサンプルの平均値が特定の値を取りうるかの検定はt検定を用いる。

Rを用いて，平均値の大小比較のt検定を行なう場合は以下の手順による。

  1. 2組のサンプルの各要素が1対1対応するものどうしか吟味する

  2. 対応するものどうしなら 「対応のある2組の平均値の差の検定」を，ないものどうしなら 「対応のない2組の平均値の差の検定」を行なう。

対応のある2組の平均値の差の検定

実験などで，同じ被検者に対して何か1つだけ条件を変えて同じ 作業をやらせたような場合，あるいは同一の機械のあるひとつの部品だけを 変えて同じことの測定を行なったような場合は，各測定値に対応が「ある」。

このような場合，同じ大きさの標本が2つあることになる。 Rでは，t.test() 関数に標本を含む2つのベクトルと paired=T 引数を与えることで検定できる。

例題

8人の被験者が公益軒とかんかんラーメンの激辛プリンを 試食し，以下のような得点をつけた。

被験者公益軒かんかん
19095
27580
37580
47580
58075
66575
77580
88085

2店の激辛プリンの評価に有意な差が認められると言ってよいか。

まず，店舗ごとの評価をベクトル化して変数に代入しておく。

koeki.pudding <- c(90,75,75,75,80,65,75,80)
kankan.pudding <- c(95,80,80,80,75,75,80,85)

この検定では以下の仮説を置く。

これを有意水準5%(0.05)で検定する。

t.test() 関数による検定

先に述べたとおり対応のある2組の平均の差の検定は， t.test() に paired=T を与えればよい。

t.test(koeki.pudding, kankan.pudding, paired=T)

  Paired t-test

data:  koeki.pudding and kankan.pudding 
t = -2.9656, df = 7, p-value = 0.02094
alternative hypothesis: true difference in means is not equal to 0 
95 percent confidence interval:
 -7.8633933 -0.8866067 
sample estimates:
mean of the differences 
                 -4.375

自由度7(df=7)のt値が-2.9656で，このときのp値は約0.02，つまり2%であり， ここまで読んで有意水準5%では棄却されることが分かる。 95%信頼区間が -7.86 〜 -0.89 であるから，本来の平均の差の値は， 95%の確率でその範囲内に入る。つまり95%の確率で 「差が0であることにはならない」ということが言える。

t値を求めた手動検定

各測定値の差をもとに，実際にt値を計算して検定して確認してみる。

復習

変数 x の各種統計量を求める関数は以下のとおり。

平均mean(x)
分散var(x)
大きさlength(x)

対応のある2組の平均値のt値は以下のように求められる。

\(t={\bar{X}-\mu\over{\sigma/\sqrt{n}}}
= {\bar{X}-\mu\over{\sigma}}\times \sqrt{n}
\)

ただし，

$\bar{X}$ : 平均
σ: 標準偏差(不偏分散の平方根，推定標準偏差)
$\mu$ : (推定)平均
n: 標本の大きさ

である。

まず，各店の激辛プリンの評価点の差を保持するベクトルを作る。

diff <- koeki.pudding-kankan.pudding
diff
[1]  -5  -5  -5  -5   5 -10  -5  -5

このベクトルから，式[1] に従いt値を求める。

n <- length(diff)
(mean(diff) - 0)/sd(diff)*sqrt(n)
[1] -2.965615

-2.965615は，t.test() が出したt値と一致する。 自由度7のt分布で，t≦-2.965615 となる確率は，pt() 関数で求められる。

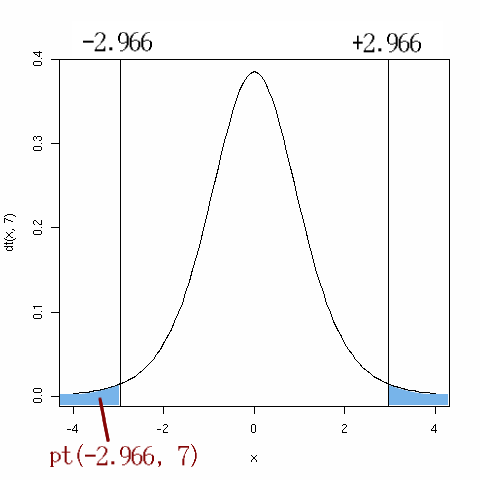
激辛プリン t値

pt(t値, 自由度) とすると，指定した自由度で 指定したt値以下を取る確率が求められる。今回は両側検定なので 値を2倍して

2*pt(-2.965615, 7)
[1] 0.02093757

となる。

ところで，式[1]の最初の分母である σ/√n のσは， 推定標準偏差であるから

$\sigma =
\sqrt{\sum(x_i-\bar{x})^2 \over n-1}
$

である。したがって

\begin{eqnarray*}
\sigma/\sqrt{n} & = & \sqrt{\sum(x_i-\bar{x})^2 \over n-1}\sqrt\frac{1}{n}\\
 & = & \sqrt{\sum(x_i-\bar{x})^2 \over n(n-1)} \\
 & = & \sqrt{\sum(x_i-\bar{x})^2 \over n}\sqrt\frac{1}{n-1} \\
 & = & s / \sqrt{n-1}
\end{eqnarray*}

(sは標本標準偏差)となり，これは 対応のある t検定と対応のないt検定の式と一致する。

対応のない2組の平均値の差の検定

公益軒とかんかんラーメン のカレーラーメンの味について，無作為抽出して採点したもらった 8人×2組のデータについて考える。

カレーラーメン評価表
公益軒点数かんかん点数
170185
275280
370395
485470
590580
670675
780780
875890
平均76.88平均81.88

2組のデータに1〜8の番号がついているが，これらは同じ番号でも 互いに全く関連がないことに注意する。

帰無仮説，対立仮説を以下のように定める。

対応のない2組の平均値の差の検定については， t.test() 関数で求める方法を示すに留める。

t.test() 関数による検定(独立2群)

以下の手順で検定を行なう。

ブラウザの表をコピーしてRのtableに読み込んで作業する例を示す。

  1. 上のカレーラーメン評価表の評価者1から評価者8までの行を すべて選択してクリップボードにコピーする。

  2. read.table("clipboard") でどうなるか視認する。

    read.table("clipboard")
  V1 V2 V3 V4
1  1 70  1 85
2  2 75  2 80
3  3 70  3 95
4  4 85  4 70
5  5 90  5 80
6  6 70  6 75
7  7 80  7 80
8  8 75  8 90

  3. 第2列と第4列に各店舗の評価ベクトルが入るので 2,4列を抽出したものを変数に代入する。

    curry <- read.table("clipboard")[,c(2,4)]
curry
  V2 V4
1 70 85
2 75 80
3 70 95
4 85 70
5 90 80
6 70 75
7 80 80
8 75 90

  4. (やらなくてもよいが)わかりやすいようラベルをつけ直す。

    names(curry) <- c('koeki', 'kankan')
curry
  koeki kankan
1    70     85
2    75     80
3    70     95
4    85     70
5    90     80
6    70     75
7    80     80
8    75     90

    これで店ごとの評価点ベクトルをそれぞれ curry$koeki, curry$kankan で取り出せる。 curry[,1]，curry[,2] でもよい。

以上の手順で必要なデータがデータフレームに得られた。

2店舗の評価点を t.test() 関数に渡す。 2つのベクトルに加え，var.equal=T を与えると「対応のない2組の平均値の差」の 検定となる。

t.test(curry$koeki, curry$kankan, var.equal=T)

  Two Sample t-test

data:  curry$koeki and curry$kankan
t = -1.2881, df = 14, p-value = 0.2186
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
 -13.325244   3.325244
sample estimates:
mean of x mean of y
   76.875    81.875

t値は-1.29，自由度14でのこのときのp値は0.219(=21.9%)なので 帰無仮説は棄却されない。つまり，有意な差があるとは言えない。

Welchの検定

ラーメンの味の評価は，点数の分布状況が等質であることが予想できる。 このような場合には，上で説明した「対応のある2組の平均の差の検定」， 「対応のない2組の平均の差の検定」いずれかを用いるのが妥当である。

いっぽう等質であると言えない場合はWelchの検定を用いる。 Rでは t.test() で2ベクトルと var.equal=F, paired=F を与えるとWelchの検定を行なう。 t.test() に2ベクトルを与えたときのデフォルトでもある。

表: カレーラーメン評価表 の調査と同時期に，かんかんらーめんのカレーラーメンを 別の箇所で無作為抽出で試食者を選び評点を集めていた。

カレーラーメン評価(2)
(かんかんラーメンは別箇所調査)
公益軒点数かんかん点数
1709100
2751080
3701198
4851290
5901380
6701465
7801550
8751690
平均76.88平均81.63
母分散49.61母分散253.48
不偏分散56.70不偏分散289.70

このかんかんラーメンの調査者は，平均は同様だが評価点のバラツキが 他箇所での調査より大きいことが分散の大きさから見て取れる。

このような場合は，Welchの検定を行なう。

t.test() 関数による検定(独立2群，分散非等質)

表カレーラーメン評価(2) の 2行目から9行目(得点のある行すべて)を領域選択でコピーし， 2列目と4列目のみ取り出したデータフレームを作る。
(領域コピーしてから以下の操作) 

(cur2 <- read.table("clipboard")[,c(2,4)])
  V2  V4
1 70 100
2 75  80
3 70  98
4 85  90
5 90  80
6 70  65
7 80  50
8 75  90

分散が等質であるかは var.test() 関数で行なえるが， 近年，等分散検査をせずにWelchの検定を行なうのがよいという説が 有力になりつつある (→ 二群の等分散性の検定)。 

# 公益軒の評点の分散
var(cur2[,1])
[1] 56.69643
# かんかんの評点(その2)の分散
var(cur2[,2])
[1] 289.6964

# 2つの分散が等しいかの検定(F検定)
var.test(cur2[,1], cur2[,2])

  F test to compare two variances

data:  cur2[, 1] and cur2[, 2] 
F = 0.1957, num df = 7, denom df = 7, p-value = 0.04711
alternative hypothesis: true ratio of variances is not equal to 1 
95 percent confidence interval:
 0.03918185 0.97755266 
sample estimates:
ratio of variances 
         0.1957098

p値 0.047(=4.7%)なので，分散は等しいとは言えない。

2つの標本の平均値が等しいかをWelchの検定で行なう。

t.test(cur2[,1], cur2[,2], var.equal=F)
  Welch Two Sample t-test

data:  cur2[, 1] and cur2[, 2] 
t = -0.7219, df = 9.639, p-value = 0.4875
alternative hypothesis: true difference in means is not equal to 0 
95 percent confidence interval:
 -19.486414   9.986414 
sample estimates:
mean of x mean of y 
   76.875    81.625

分散の等質性(分布の同様性)があることが明らかでない場合や， 2群のサンプルサイズが等しくない場合には，最初からWelchの検定を 行なってよい。Rの t.test() 関数のデフォルトに従うのが賢明な選択と言える。

片側検定・両側検定

平均が異なるかどうかを吟味するのは両側検定である。 2組の平均のどちらかがもう片方より大きい(あるいは小さい)かどうかを 吟味する場合は片側検定を行なう。Rではこの場合，関数の 引数に alternative="……" を与えて切り替えを行なう。 代入する値は "greater", "less" のいずれかである。

公益軒ではカレーラーメンをもっとヒットさせるべく， 味の改良を行なった。しかし本当に受けがよいのか調べるため， ある日の客20人を無作為に選び， 全く同じカレーラーメンという名前で旧版と新版をそれぞれ 10人ずつに食べてもらい，評点をつけてもらった。 そのときの結果が以下の表である(番号は単なる数え上げで， 同じ番号どうしの客に関連はない)。

新旧カレーラーメン評価表
旧点数新点数
165190
270250
375370
480490
585575
660675
770785
880890
970995
10701040
平均76.88平均81.88

一見新カレーラーメンの方が良さそうだが，偶然甘い評価をする人々に 当たっただけということはないだろうか。

単に，評価が違うことを検定するのであれば帰無仮説と対立仮説を 以下のように据える(両側検定)。

しかし，帰無仮説が棄却されたとしても，「評価が違うらしい」 という結論が得られても店にとってはうれしくない。ここは 「新ラーメンの方が高い評価である」と大小をはっきりさせたい。

このような場合は，棄却域を片側だけに取る。

帰無仮説の棄却域5%を分布の片側だけに持って来る。 この場合，対立仮説で第1引数(旧ラーメン)が第2引数(新ラーメン) より小さくあってほしいので t.test() に alternative="less" を与える。以下実行例を示す。

# 新旧カレーラーメン評価表の評点部分を領域をコピーしてから
newc <- read.table("clipboard")[,c(2,4)]
newc
   V2 V4
1  65 90
2  70 60
3  75 80
4  80 95
5  85 75
6  60 85
7  90 95
8  80 90
9  70 95
10 70 40
t.test(newc[,1], newc[,2], alternative="less")

  Welch Two Sample t-test

data:  newc[, 1] and newc[, 2]
t = -0.9364, df = 13.447, p-value = 0.1828
alternative hypothesis: true difference in means is less than 0
95 percent confidence interval:
     -Inf 5.318399
sample estimates:
mean of x mean of y
     74.5      80.5

これによると，第1引数(旧)のほうが第2引数(新)より高い平均値を 持つ場合でも，このような結果が約18%程度は出ることが分かり， 帰無仮説は棄却されない。

確実にヒットをねらうなら，より高い評価が得られる改良をすべきだろう。

練習問題

チーズラーメンの問題

新製品のチーズラーメンの評価を集めた。

公益軒の
試食者		評点 かんかんの
試食者		評点
180175
275265
380380
495485
590575
680680
785780
890870

この調査結果をもとにして，両店舗の評価を比較したい。 以下の問に答えよ。

  1. 店ごとの評点の平均と分散を求めよ。
  2. 帰無仮説を立てよ。
  3. 対立仮説を立てよ。
  4. 分散の違いについて吟味せよ。
  5. Rを用いて検定せよ。

帰無仮説=「両店舗のチーズラーメンの評価に有意な差はない」

(cheese <- read.table('clipboard')[,c(2,4)])
  V2 V4
1 80 75
2 75 65
3 80 80
4 95 85
5 90 75
6 80 80
7 85 80
8 90 70
t.test(cheese[,1], cheese[,2])

        Welch Two Sample t-test

data:  cheese[, 1] and cheese[, 2] 
t = 2.4631, df = 13.956, p-value = 0.02740
alternative hypothesis: true difference in means is not equal to 0 
95 percent confidence interval:
  1.04779 15.20221 
sample estimates:
mean of x mean of y 
   84.375    76.250

棄却。

チーズラーメンの問題・続編

上の問のチーズラーメンの試食者の各番号を振られた人が、 どちらも同一人物だった場合はどうなるか。前問と同じ流れで検定せよ。

検定関数の t.test に paired=T を追加すればよい。

ダイエット食品の問題

ある番組でこのような結果提示ががあった。

10人の被験者を5人ずつの2グループA，Bに分けてダイエット実験をした。 グループAの人にはダイエット薬と称してこんにゃく粉末を， グループBの人には「んめちゃダイエット」を，いずれも10日間摂取させ 体重の増減を調べた。10人の実験前後の体重減少(kg)は以下のとおりであった。

こんにゃく粉末んめちゃダイエット
1.63.3
2.14.9
2.52.9
-2.42.2
3.1-0.1
平均
1.382.64

この結果を得て，司会者は「最も効果のあった人は5kg近く， それに平均でなんと2倍ものダイエット効果があります!」と結論づけた。

この商品の宣伝文句に偽りなし，といってよいだろうか。

  1. 帰無仮説を立てよ。

  2. 対立仮説を立てよ。

  3. Rを用いて検定せよ。

(上の表のデータ部分を領域選択してから)

nme <- read.table("clipboard")
# x=「こんにゃく」，y=「んめちゃ…」とすると，
# 対立仮説は x-y < 0 なので alternative="less"
t.test(nme[,1], nme[,2], alternative="less")

  Welch Two Sample t-test

data:  nme[, 1] and nme[, 2]
t = -0.9903, df = 7.755, p-value = 0.1760
alternative hypothesis: true difference in means is less than 0
95 percent confidence interval:
     -Inf 1.115817
sample estimates:
mean of x mean of y
     1.38      2.64

p値が約0.18=18%なので，「んめちゃ…」が優れていなくても同様の実験を 5〜6回行なえば1回はこのような結果が得られる程度の事象でしかない。よって， 賢明な視聴者は飛びつかない方がよい。

今週の課題

問題

第4回 t検定 の[14]のレポート課題(2問とも)を，Rを用いて解け。 計算に関る手順はすべてRに任せてよい。

提出方法

宛先 sip-12-21@e.koeki-u.ac.jp

締切 6日後

Subjectに Student test と書き，本文の先頭に 氏名，学籍番号を入れ，その後の本体を以下のようにする。

解答の検定部分は，Rに対する入力と出力を本文内に貼り付ける。 ただし，検定の手順に関する言葉は正確に記述すること。

各設問に対する解答は，

  1. どの検定手法を用いるべきか
  2. 帰無仮説と対立仮説
  3. Rでの検定結果

を詳しく記述すること。

yuuji@e.koeki-u.ac.jp