あなたはかんかんラーメンの経営者である。かんかんラーメンの売りはカレーラーメンである。しかし、カレーラーメンに目をつけた他の店も真似をしてくるようになり、最近ではライバル店の公益軒の方が売り上げが良いように思える。そこで、かんかんラーメンのカレーラーメンは本当に売り上げが悪いのかを調べることにした。以下が1日の売り上げ数である。

	しょうゆラーメン	カレーラーメン	合計
かんかんラーメン	435	165	600
公益軒	265	135	400

この表によると、かんかんのカレーラーメンの売り上げは165杯で、公益軒のカレーラーメンの売り上げは135杯である。単純に数を比較すればかんかんラーメンのカレーラーメンの方が売れているということになる。しかし、公益軒を訪れる客が好んでカレーラーメンを食べているということになると話は別である。この場合、カレーラーメンを求めて公益軒を訪れていることになり、将来的には順位が逆転する恐れがあるからである。公益軒を訪れる客は好んでカレーラーメンを注文しているのかどうかを明らかにするためには、単純に165杯と135杯を比較しても意味がない。そこで、定番メニューのしょうゆラーメンを基準として比べることにした。

すると、かんかんではしょうゆラーメン435杯に対してカレーラーメン165杯で約4割であった。一方公益軒ではしょうゆラーメン265杯に対して、カレーラーメン135杯で約5割となっている。比率を見る限り、公益軒のカレーラーメンの方が好まれているように見える。

この結果をもとに、公益軒の方がカレーラーメンを求めて訪れる客が多いと断言してよいだろうか。

両者の差について検討する場合、統計学ではまず仮説を立てるところから出発する。そして、その仮説が正しいかどうかを検証することになる。この場合、以下のような仮説を立てることができる。

かんかんラーメンと公益軒では、しょうゆラーメンとカレーラーメンの売り上げの割合に差はない。

仮説を立てる場合、まずは「差はない」という仮説を立てる。これを帰無仮説という。「差がない」という仮説は非常に単純であり、この仮説が肯定されれば差がないことになる。また否定されれば差があることになる。一方で「差がある」という仮説を立てた場合、差の出方は多様である。「差がある」という仮説が否定された場合、大きな差がないだけなのか、中程度の差ならあるのかと、解釈が難しくなる。差がある場合では差の程度についても考える必要が出てくるが、差がないという仮説であれば、肯定するか否定するかだけなので非常に単純である。なお、帰無仮説の反対の仮説のことを対立仮説という。また、仮説を肯定することを「採択する」とよび、否定することを「棄却する」という。

これらをまとめると以下のようになる。

• 「〜は差がない」という帰無仮説を立てる
• 帰無仮説を採択するか、棄却するかを決める
• 帰無仮説を採択した場合は「差がない」という結論になる
• 帰無仮説を棄却した場合は対立仮説が採択され「差がある」という結論になる

では、帰無仮説を採択するか、棄却するかをどのようにして決めればよいだろうか。統計学では採択できるかどうかを確率で計算する。もしも2群を比較する場合、両者に差がないのであれば、両者の差は偶然に発生したということになる。サイコロ10個を2回振っても合計が同じ数にならないように、偶然にある程度の誤差は生じる。そこで、2群の差が偶然に発生するとした場合に、その差が偶然に発生しうる確率はどれくらいであるかを計算で求める。2群の差が小さければ、その程度の差は頻繁に発生するであろうし、かなり差が大きいのであれば偶然にそのような差が生じる可能性は少ないかもしれない。

比較したい対象の差が偶然に発生する確率が5%以下である場合、偶然にそのような差が発生する確率は非常に低く、偶然による差では説明ができないとみなす。つまり「差はない」という帰無仮説を棄却し、「差がある」という対立仮説を採択する。なお帰無仮説を採択もしくは棄却する基準となる5%のことを、有意水準5%とか危険率5%と呼ぶ。場合によっては5%ではなく1%を基準として用いることがある。確率が5%以下であれば帰無仮説を棄却してよいが、確率が1%よりも小さいということであれば、2群に見られた差は偶然に発生する確率は1%以下ということになり、5%以下であるという場合よりも説明力が強くなる。このため、基準として1%を用いることもある。

期待度数を求める

先ほどカレーラーメンの比較をする際に立てた帰無仮説を採択することができるかどうか検討しよう。このために、まずかんかんも公益軒もしょうゆラーメンとカレーラーメンが全く同じ割合で売れるとした場合の売り上げ数を計算してみよう。それぞれのお店の合計の売り上げ数と、しょうゆラーメン、カレーラーメンの合計の売り上げ数がわかれば、同じ割合で売れるとした場合の数を計算で求めることができる。

まず、かんかんと公益軒の売り上げは合計でそれぞれ600杯、400杯である。つまり売り上げ数は600：400で表現できる。ここで、しょうゆラーメンは両店合計で700杯売れているので、同じ割合で売れているとするならば、600：400＝3：2の割合になるはずである。これを求める式は以下の通り。

• かんかん：700÷1000×600＝420
• 公益軒：700÷1000×400＝280

カレーラーメンは合計で300杯売れているので、両店が同じ割合で売れているとすれば、3：2で配分されるはずであり、以下の式で計算すればよい。

• かんかん：300÷1000×600＝180
• 公益軒：300÷1000×400＝120

結果的に、同じ割合で売れるとした場合の売り上げ数は以下のようになる。この個数を期待度数という。両店の売り上げの割合に差がないのであれば、期待度数のようになるはずである。しかし実際には、若干期待度数からは値がずれている。ちなみに実際の値のことを観測度数と呼ぶ。

	しょうゆラーメン	カレーラーメン	合計
かんかんラーメン	420	180	600
公益軒	280	120	400
合計	700	300	1000

期待度数と観測度数を比較してみると次のことがわかる

• かんかんのしょうゆラーメンは実際の方が多い（＋15杯）
• かんかんのカレーラーメンは実際の方が少ない（-15杯）
• 公益軒のしょうゆラーメンは実際の方が少ない（-15杯）
• 公益軒のカレーラーメンは実際の方が多い（+15杯）

このような状況において帰無仮説が採択できるかどうかは、15杯のずれというのが偶然に発生するとした場合、比較的頻繁に（少なくとも5%以上の確率で）発生するものかを明らかにすることにより検討することができる。

期待度数からのずれを計算する

観測度数が期待度数からどの程度ずれているのかを計算してみよう。

この場合、単に期待度数と観測度数の差を取って総和を求めてもプラスとマイナスが打ち消しあって0になってしまう。

(435-420)+(165-180)+(265-280)+(135-120)=0

これではまずいので、マイナスをなくすために、標準偏差を計算する場合同様に2乗してみよう。これで0にならなくなった。

(435-420)²+(165-180)²+(265-280)²+(135-120)²=900

しかし、これでもまだ問題がある。仮に2日分の売り上げ数のデータを得た場合、全ての値が2倍になるが、その値に基づいて行った計算結果を見てみよう。

(870-840)²+(330-360)²+(530-560)²+(270-240)²=3600

結果は900から3600というように4倍になってしまっている。このままではずれの大きさがデータ数に依存してしまうので、（観察度数−期待度数）²を期待度数で割っておくことにしよう。

（（（観測度数−期待度数）の２乗）÷期待度数）の総和

(435-420)²/420+(165-180)²/180+(265-280)²/280+(135-120)²/120

=15²/420+(-15)²/180+(-15)²/280+15²/120

=0.536+1.250+0.804+1.875

=4.464

これをχ2乗値（カイ2乗値）と呼ぶ。もう一度まとめると、

カイ２乗値＝（（（観測度数−期待度数）の２乗）÷期待度数）の総和

になる。期待度数と観察度数が一致する場合はχ2乗値は0になり、ずれが大きくなるほど、χ2乗値は大きくなることがわかる。

χ2乗値が4.464になったということは、ある程度ずれがあることを示している。では、この値は偶然に発生する可能性は何%くらいなのであろうか。そのためにはχ2乗値の性質を調べておく必要がある。

以下はχ2乗値の分布である。とりあえずは自由度1のピンク色の線を見てみよう。もしも、2群には実際には差がなく、観察度数の期待度数からのずれが偶然に発生したものである場合、χ2乗の値は小さくなるはずである。ピンク色の線を見た場合、χ2乗値が小さい部分の分布が多くなっている。偶然にχ2乗値が大きくなる（=観察度数と期待度数のずれが大きくなる）こともあるが、その確率は非常に小さい。

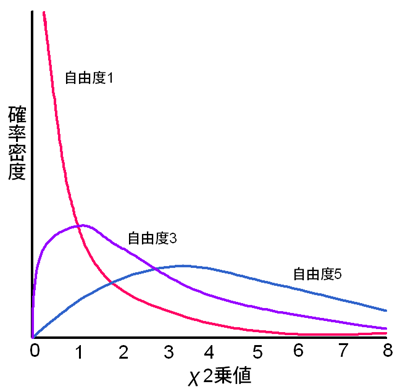
ただし、χ2乗分布は条件の数に依存する。この例ではしょうゆラーメンとカレーラーメンの2条件で検討しているが、もっと条件を多くした場合を考えてみよう。仮に、しょうゆラーメン、カレーラーメン、塩ラーメン、味噌ラーメン、チャーシューメン、タンメンの6条件の場合はどうだろうか。この場合、全ての観察度数が期待度数と一致することの方が奇跡的であり、ある程度はずれが生じることが予測される。χ2乗値が0というのはほとんど起こりえず、若干大きい値になる場合が多いはずである。

上の図では、3本の曲線が引かれているが、それぞれ「自由度1」「自由度3」「自由度5」と書かれている。かんかんラーメンは総売上数が600杯である。このため、しょうゆラーメンの売り上げ数がわかれば、カレーラーメンの値は自動的にきまる。つまり2種類の値のうち、自由に動かせるのは一つだけになる。この数を自由度と呼ぶ。2条件の場合は2-1で自由度は1になる。また6条件の場合は6-1で自由度は5になる。自由度5の青色の線を見てみると、ある程度χ2乗値が大きいところに分布の山ができていることがわかる。

ではχ2乗検定を行って、かんかんと公益軒の売り上げの割合に違いがあるかを考えてみよう。χ2乗値は4.464であった。では自由度はいくつになるだろうか。この場合は、かんかんのしょうゆラーメンの売り上げ数がきまれば、かんかんのカレーラーメンと公益軒のしょうゆラーメンの売り上げ数がきまる。それに伴って公益軒のカレーラーメンも求まる。このため自由に設定できる値は1つである。これは以下の式で計算できる

i行j列の表における自由度の計算

• 自由度=(i-1)×(j-1)

さて、自由度が1、χ2乗値が4.46となった。ではこの値が偶然に発生する確率は何%程度あるのだろうか。自由度とχ2乗値がわかると、それが起こる確率を調べることができる。その場合、χ2乗分布表を使うと便利である。

自由度	5%	1%
1	3.84	6.63
2	5.99	9.21
3	7.81	11.34
4	9.49	13.28
5	11.07	15.09

自由度が1のχ2乗分布を考えると、以下のようになる。5%のχ2乗値が3.84である。これは、χ2乗値が偶然に3.84よりも大きい値になる確率が5%であると読む。同様にχ2乗値が6.63よりも大きい値になる確率が1%であると読む。

今回は「かんかんラーメンと公益軒では、しょうゆラーメンとカレーラーメンの売り上げの割合に差はない。」という仮説（帰無仮説）を立てた。この仮説が正しければ、両者の差は偶然に発生したものになるため、差が偶然に発生する確率をχ2乗値を元に計算したが、χ2乗値は4.464となり、これは3.84よりも大きく6.63よりも小さかった。つまり、この仮説を支持できる確率は1%以上5%未満ということになる。5%未満の確率でしか発生しない場合、既に説明したとおり、偶然に発生した差であると言うことはできないとみなす。したがって今回の結果からは以下の結論が導き出せる。

• 仮説として「かんかんラーメンと公益軒では、しょうゆラーメンとカレーラーメンの売り上げの割合に差はない。」とした。
• χ2乗値は4.464となり、これが発生するのは5%より低い確率であった。
• これは偶然ではめったに発生しないことであるといえる。
• したがって、帰無仮説は棄却される。
• これに伴い、対立仮説が採択され、かんかんラーメンと公益軒ではしょうゆラーメンとカレーラーメンの売り上げの割合に差があると結論づけることができる。

参考までにχ2乗分布表の5%、1%の値は表計算ソフトではCHIINVという関数を用いて求めることができる。以下に5%の値、1%の値の算出方法を示す。

• 基本構造：=CHIINV(確率,自由度)
• 5%の値：=CHIINV(0.05,自由度)
• 1%の値：=CHIINV(0.01,自由度)

今回は2×2の表を用いた例を示したが、χ2乗検定はi×jの表（任意の表）に適用することができる。ここでは、先ほどの例に新製品のチーズラーメンを加えた結果に基づいてχ2乗検定を適用してみよう。

	しょうゆラーメン	カレーラーメン	チーズラーメン	合計
かんかんラーメン	435	165	650	1250
公益軒	265	135	350	750
合計	700	300	1000	2000

χ2乗検定を実施して結論を導き出すための手順は以下の通りである。順番に実施してみよう。

1. 帰無仮説を立てる
2. 対立仮説を立てる
3. 期待度数を計算する
4. χ2乗値を計算する
5. 自由度を求める
6. χ2乗分布表を調べる
7. 計算したχ2乗値と表の値を比較する
8. 結論を述べる

結果の記載方法

レポート等でχ2乗検定を実施した結果を記述する場合、記載すべき項目が定められている。以下に例を示すので、今後レポートを作成する際には参考にしよう。

表○は、かんかんラーメンと公益軒のしょうゆラーメンとカレーラーメンの売り上げ数を示したものである。χ²検定の結果、売り上げ数の割合の偏りは有意であった(χ²(1)=4.464, p<.05）。

なお、χ²(1)の(1)は自由度をあらわす。

また、p<.05は5%水準で有意であったことを示す。1%水準で有意であった場合はp<.01、確率が5%よりも大きかった場合（=有意でない場合）は、p>.05またはn.s.と記す。後者はnot significantの略である（significantは「有意｣の意）。

有意：偶然に発生した差ではなく意味の有る差であるという意味

A市、B市、C市の3つの市で、現在の生活に満足しているか質問を行った。以下の表がその結果であるが、市によって「満足」「どちらでもない」「不満」の回答率に偏りがあるといえるか。

	満足	どちらでもない	不満	合計
A市	45	45	60	150
B市	30	40	80	150
C市	35	30	35	100
合計	110	115	175	400

この問題について、以下の流れで検定を行い結果をまとめなさい。1〜8まですべてエクセルファイル内に記載すること。体裁は自由とするが1つのワークシートに読みやすくまとめること。

1. 帰無仮説を立てる
2. 対立仮説を立てる
3. 期待度数を計算する
4. χ2乗値を計算する
5. 自由度を求める
6. χ2乗分布表を調べる
7. 計算したχ2乗値と表の値を比較する
8. 結論を述べる

提出要領

• To: naoya @ e.koeki-u.ac.jp（@前後のスペースを除去すること）
• Subject: 社会情報処理(3)
• 提出期限：次回授業開始時まで
• ファイルを添付して送ること。ファイル名は学籍番号-shakai3.xls