データを取扱う際は尺度に注意する必要がある。データは尺度により特徴が異なり、利用できる統計的な手法も異なる。

名義尺度（nominal scale）

質的な変数による分類の尺度。「はい」「いいえ」、「男性」「女性」、「英語」「数学」「国語」などの分類が該当する。ここではカテゴリ間の大小関係は想定されていない。名義尺度では、各カテゴリが全体に占める比率が主な統計的処理となる。

順序尺度（ordinal scale）

質的な変数により順序が示されている場合は順序尺度となる。「優」「良」「可」や「1位」「2位」「3位」などが該当する。優は良より優れ、良は可より優れているという順序は定められているが、優と良の間の開きと、良と可の間の開きは必ずしも等間隔ではない。データの等間隔性が保証されていないため、平均値を求めてもあまり意味がない。順序尺度では、中央値やパーセンタイル、四分位偏差、ノンパラメトリック検定が適用される。

距離尺度（もしくは間隔尺度：interval scale）

距離関係が等しく保持された量的尺度。原点が任意の位置に定められているのが特徴であり、例えばテストの得点が該当する。テストで0点であることが、学力がゼロであることを意味しないし、100点取れた人は、50点の人の2倍の学力を有するということにもならない。距離尺度では、平均値、標準偏差、ピアソンの積率相関係数、t検定、分散分析、回帰分析などほとんど全ての統計的分析が適用できる。

比率尺度（もしくは比例尺度：ratio scale）

データの等間隔性が保持され、原点の0が無の状態を表す量的尺度。時間、重さなど様々な測定値が該当する。原点の0が意味を持つため、比例関係を考えることができる。つまり30分は10分の3倍であり、100mは10mの10倍になる。比率尺度は、距離尺度同様ほとんど全ての統計的分析を適用できる。量的な尺度として距離尺度と比率尺度は統計的処理を行う上で実質的に差はないと考えてよい。

• 記述統計学：調査等によって得られたデータの特徴を記述するための方法論。度数分布、平均値、中央値、最頻値、分散、標準偏差、四分位偏差、尖度、歪度、相関、連関等がある
• 推測統計学：標本から母集団の統計的性質を推測するための方法論。χ²検定、F検定、t検定、分散分析、マンホイトニー検定、符号付順位検定、フリードマン検定等がある

調査等を行う場合、一般に対象者は限定される。例えば選挙前になると支持政党に関する電話調査が頻繁に行われる。回答数は500人程度であるが、我々はこの500人の結果そのものに関心があるわけではない。500人の結果を通して有権者の全体傾向を知りたいのである。

有権者全体の意識を明らかにするためには全員に聞くのが確実である。しかし、現実的に全数調査は不可能であるため、一部の人に対する調査結果をもとに、全体傾向を推定する。

ここで、選出された一部の人達のことを標本と呼ぶ。一方、実際に検討しようとしている対象全体（ここでは有権者全体）を母集団と呼ぶ。

標本の抽出は無作為に行う必要がある。支持政党に関して言えば、農村部は自民党支持、都市部は民主党支持というような傾向があるため、特定の地域を対象に調査を行い、それが全有権者の一般傾向であると結論づけるのは無理がある。

標本が母集団を代表していることを保証するためには、恣意的に抽出するのではなく、無作為に抽出すればよい。母集団が1000人の場合は一人一人に1〜1000の通し番号をつけ、乱数表を用いてランダムに数字を選びその番号に当たる人を標本とする方法を単純無作為抽出法と呼ぶ。

母集団から標本を取り出して平均値や標準偏差を求めた結果は、母集団の平均や標準偏差と等しいといえるだろうか。100人の母集団から10人の標本を取り出した場合を例にとって確認してみよう。

sip1.xls

母集団と標本の関係

データ処理の結果分かることは次の通り。

• 標本の平均は母集団の平均の推定値として使用できる
• 標本の標準偏差は母集団の標準偏差よりも小さくなる

母標準偏差と標本標準偏差

標本の標準偏差（標本標準偏差）は母集団の標準偏差（母標準偏差）よりも小さくなる。よって、標本から母集団の標準偏差を推定するためには、標本標準偏差よりも少し大きな値にしなければならない。具体的には次式を用いる。

表計算ソフトを用いて標準偏差を計算する場合、母標準偏差はSTDEVP、標本標準偏差はSTDEVを用いる。

なお、標本の平均は母集団の平均値として使用可能であるが、抽出した標本により、母集団の実際の平均値とは若干異なる結果になる場合が多い。このため、実際には標本の平均は母集団の平均とは等しくならない。

上記の例では標本を10回抽出し、それぞれ平均値を求めたが、仮に母集団の人数が非常に多く、その母集団に対して10個ずつ標本を取り出して平均を求めるという作業を延々と繰り返した場合、以下の図ような分布になると考えられる。

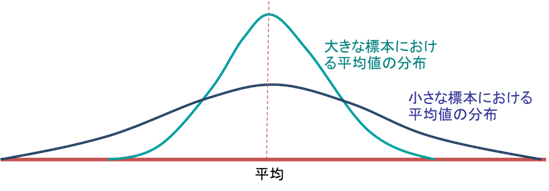
• 平均値は母集団全体の平均に近い場合が多いが、時として母集団からかなり外れた値が平均値となることがある
• 標本の数が少ない場合（例：10個の場合と5個の場合）は平均値に対する個別のデータの影響が大きくなるため分布は広くなる

母集団が正規分布に従う場合、標本平均の分布も正規分布に従う。ただし、この分布の広がり具合は標本の大きさにより変化する。つまり

• 標本が大きい場合は分布が狭くなる
• 標本が小さい場合は分布が広くなる

という特徴を持つ。ここで分布の広がり具合は分散もしくは標準偏差で表現可能であり、いずれも値が大きい場合は分布が広く、小さい場合は狭いことを意味する。なお、分散と標準偏差の間には、分散＝標準偏差の2乗（標準偏差＝√分散）という関係がある。

この標本平均の分布をt分布と呼び、その分散は次式で表現できる。

標本平均の分散＝母集団の分散/標本の大きさ（データ数）・・・(1)

信頼区間の考え方

抽出された標本の平均値は分布の中のどこかに位置することになる。平均付近に位置することが多いが、場合によっては周辺に偏ることもある。そこで、母集団の平均を示す際には、平均が含まれる範囲を示すという方法がとられる。

そして、範囲は一般的には「95％の確率で母集団の平均が含まれる範囲」もしくは「99％の確率で母集団の平均が含まれる範囲」を使う。前者を95％信頼区間、後者を99％信頼区間と呼ぶ。

95％信頼区間を求める際の考え方を次の図を使いながら説明する。

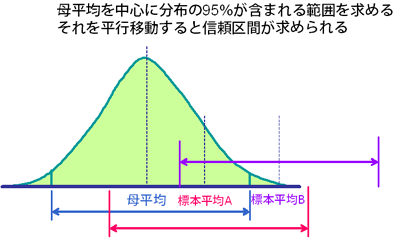
標本平均の分布は正規分布と似たt分布に従う。つまり、抽出された標本の平均値や母平均付近に位置する場合が多く、母平均から大きく外れる場合は少ない。繰り返し標本を抽出して求めた平均値の95％が含まれる範囲は、分布の左右の裾野である各2.5％を除外した範囲となる（図中青色）。

この範囲が求められたら、それを標本平均を中心とする範囲となるように平行移動してみる。標本平均が分布の裾野付近に位置しない限り、母平均は範囲内に含まれることになる（図中赤色）。仮に標本平均が分布の裾野に位置する場合、範囲内に母平均は含まれない（図中紫色）。

標本平均を基準として範囲を定めた場合に、その範囲内に母平均が含まれないのは、標本平均が左右の裾野の2.5％に位置する場合であるため、結果的にこの範囲に母平均が含まれる確率は95％となる。これが95％信頼区間である。

仮に、標本平均の99％が含まれる範囲を設定し、それを平行移動した場合は、抽出された標本の平均が左右の裾野の0.5％に位置しない限り、この範囲内に母平均が含まれることになる。つまり99％の確率で母平均が含まれることになる。これを99％信頼区間という。

では、具体的には信頼区間はどのように求めるのであろうか。これについては正規分布における標準偏差と分布の関係を確認した上で説明する。

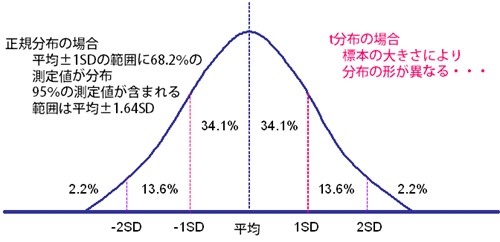
正規分布の特徴

正規分布では、平均値に対して標準偏差を加算・減算した範囲（平均値±1SD）内に68.2％の測定値が含まれるという特徴がある。また標準偏差を2倍した値を加算・減算した範囲（平均値±2SD）に95.6%の測定値が含まれる。

つまり、平均値に対して標準偏差をN倍した値を加算・減算した範囲内にP%の測定値が含まれるという特徴がある。ここで95％の測定値が含まれる範囲を求める場合、Nは1.96、99％ではNは2.58である。

t分布における信頼区間

正規分布の場合は、1.96、2.58という値は固定である。しかし、t分布の場合は標本の大きさにより分布の形が異なるため、これらの値も変化する。

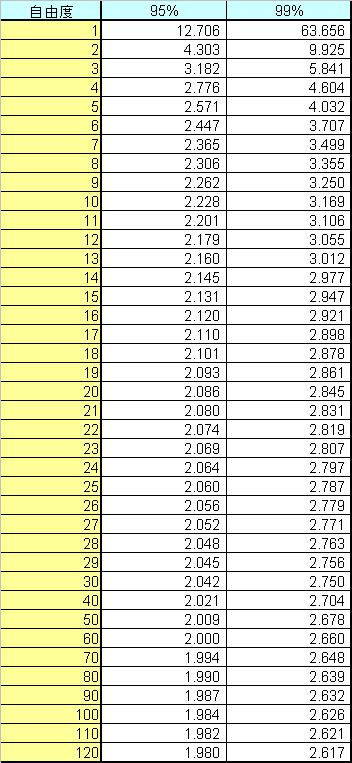
まず、t分布の場合には1.96や2.58に相当する値をt値と呼ぶ。t値は標本の大きさによって異なる。以下の表はt分布において95％、99％の範囲を求める際に使用するt値である。なお、読み取る際は標本の大きさに対応する値ではなく、標本の大きさ−1の値に対応するt値を利用する。標本の大きさ-1を自由度と呼ぶ。このため、標本の大きさが10の場合、自由度9のt値を読み取り、95%信頼区間であれば2.262、99%信頼区間では3.250を用いる。

t値は以下の表を用いる以外に、表計算ソフトで求めることもできる。t値を求める関数はTINVである。

=TINV(確率,自由度)

• 95%信頼区間のt値：=TINV(0.05,自由度)
• 99%信頼区間のt値：=TINV(0.01,自由度)

信頼区間の計算式

t値がわかれば次式で信頼区間を求めることができる

95%信頼区間=標本平均±95%のt値×標本標準誤差

99%信頼区間=標本平均±99%のt値×標本標準誤差

標本標準誤差とは、標本平均の標準偏差のことである。つまりこの式は、正規分布において平均値にN倍の標準偏差を加算・減算するのと同じ式である。なお、標本標準誤差は次のように求めることが出来る。

まず(1)式より、標本平均の分散＝母集団の分散/標本の大きさ（データ数）である。標本平均の分散の平方根が標本平均の標準偏差となる。ここで、母分散の分散は既知ではないため、標本から推定した標本標準偏差の2乗を用いると、

標本標準誤差＝（標本標準偏差の2乗/標本の大きさ）の平方根となる。ここから2乗と平方根を相殺すると

標本標準誤差=標本標準偏差/（標本の大きさの平方根）となる。

Aさんはカレー屋さんを経営している。カレーの量は200gと決めているが、時折ちょっと少ないんじゃないのというクレームが入ることがある。そこで、適正な分量のカレーが提供されているかどうか調べるため、1時間ごとに1皿取りあげ、重さを計測した。以下がそのデータである。

218
186
221
204
195
198
214
202
196

この値をもとに95%信頼区間、99%信頼区間を求めなさい。また、ここからわかることについて考えなさい。

公益食堂のハンバーグは200gであるが、実際に200gあると言えるか。ランダムに18個のハンバーグの重さを測った結果として以下の値が得られているものとして、95%信頼区間、99%信頼区間を求めた上で、200gあると言えるかどうか検討しなさい。

195	182
186	204
203	208
210	211
190	190
182	192
203	182
202	191
196	180

この問題について、エクセルのワークシートに計算式や結果、考察等を分かり易くまとめ、添付ファイルで提出しなさい。

提出要領

• To: naoya @ e.koeki-u.ac.jp（@前後のスペースを除去すること）
• Subject: 社会情報処理(2)
• 提出期限：次回授業開始時まで
• ファイルを添付して送ること。ファイル名は学籍番号-shakai2.xls