本日は前回の作業を継続する。早く終わった人は[2]の平均値の差の検定を行う。前回までの作業を念のため記載する。

前回の作業

オペレーション不安（因子1）、テクノロジー不安（因子2）、肯定的評価（因子3）の合計得点を求め、合計得点が低い50人（自信群）、高い50人（不安群）を対象にデータ処理を行う。

このデータについて、以下のデータ処理を行いグラフを作成する。最低でも4番、できれば6番まで実施してみよう。

1. 2の「基礎知識」〜「表計算」の6項目の群別平均習熟得点と平均習熟率
2. 3の各因子の群別平均得点
3. 4-1の各セキュリティリスクの群別認知率
4. 4-2の各セキュリティリスクへの対策の理解度の群別平均点
5. 上の4項目について、群別のみでなく実用情報履修者の得点を算出する（前回のワークシートからコピーすればよい）
6. 2の個別の質問項目に対する群別平均習熟率
7. 1の各データについて群別の特徴の有無を調べる

これまで学年別、自信別に各質問項目について平均値や比率を計算してきた。その上でグラフを作成し平均値が異なることを確認してきた。しかし、サイコロを10回振った場合の平均値が最初の10回と2回目の10回では異なる場合が多いように、平均は誤差を含む値である。

では、今回見られた学年別の平均値の差や、自信群と不安群の平均値の差は誤差なのだろうか？　それとも実際に差があるとみなすべきなのだろうか？　平均値の差が意味のある差（有意差）なのかどうかを検定する手法にt検定や分散分析がある。詳細は統計学で学ぶべきことであるため、ここでは3つ以上の平均値の差の比較を行う際に使用する分散分析について概略を説明し、実際に分析を行う。あわせて回答の比率の差があるかを比較する際に使用するχ²についても利用してみる。

仮設検定

平均値の差を検討する場合、統計学ではまず仮説を立てることから出発する。そして、その仮設が正しいかどうかを検証することになる。例えば次のような仮説を立てることが出来る。

自信群と不安群ではセキュリティの理解度の平均値に差はない。

まずは「差はない」という仮説を立てる。これを帰無仮説という。「差がない」という仮説が採択されれば「差がない」ということになり、否定（棄却）されれば「差がある」という結論になる。採択できるかどうかは、確率計算を行って決める。

自信群と不安群のセキュリティの理解度に差がない場合、両者の差は偶然に発生したということになる。ある程度の差は偶然でも頻繁に生じうるだろうし、大きな差でも確率は低いながら偶然に発生する可能性があるかもしれない。

比較したい対象の差が偶然に発生する確率が5％以下である場合、偶然にそのような差が発生する確率は非常に低く、偶然による差では説明が出来ないとみなす。つまり帰無仮説を棄却し、「差がある」ということになる。なお帰無仮説を採択もしくは棄却する基準となる5%のことを、有意水準5%とか危険率5%と呼ぶ。なお、1%を基準として用いることもある。1％水準は、5％水準よりも説明力が高くなる。

分散分析の考え方

3つ以上の平均値の差を比較する際に用いるのが分散分析である。例えば、自信群と不安群に実用情報履修者を加えた場合が該当する。この場合の帰無仮説は次のようになる。

自信群と不安群と実用情報履修者のセキュリティの理解度の平均値に差はない。

3群のデータはは下の図のように記述できる。ここで自信群の中のある1つのデータについて考えてみよう。データは全体の平均からずれているが、このずれは「全体の平均と自信群の平均のずれ」と「自信群の平均からのズレ」に分解できる。

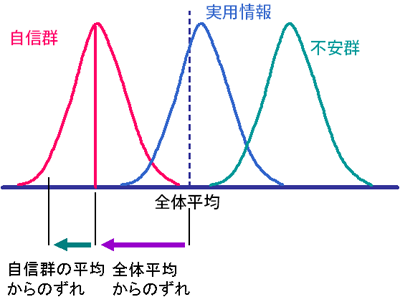
ここで「全体の平均と自信群の平均のずれ」は全体の平均から各群がどれだけずれているかをあらわしている。これを群間のズレと呼ぶ。一方、「自信群の平均からのずれ」は群の中で、個々のデータがどれだけずれているかをあらわしている。これを群内のずれとよぶ。

つまり、すべてのデータについて
全体の平均からのズレ　＝　群間のズレ　＋　群内のズレ
が成り立つ。

群間のずれが大きくなるということは、各群の平均が大きく異なるということになる。一方、群内のずれは、同じ集団内でのばらつきであり「誤差」や「個人差」として扱うことができる。もし、群内のずれに比べて、群間のずれが大きければ、集団の間の違いが大きいということになるので、「平均に差がない」という帰無仮説を棄却することになる。逆に、群内のずれに比べて、群間のすれが小さければ、集団の間の差が大きいとはいえないので、「平均に差がない」という帰無仮説を採択することになる。

分散分析の手順

今回、平均値を算出しているのは、2の平均習熟得点と3の各因子と4-2のセキュリティの理解度である。これらは分散分析を行うことが出来る。

例えば、2の平均習熟得点は6項目あるので、以下の手順を6回繰り返すことになる。厖大な作業量になるので、効率的なデータ処理をする方法を考えてみよう。

ここでは架空のデータを使って分散分析の手順を確認する。

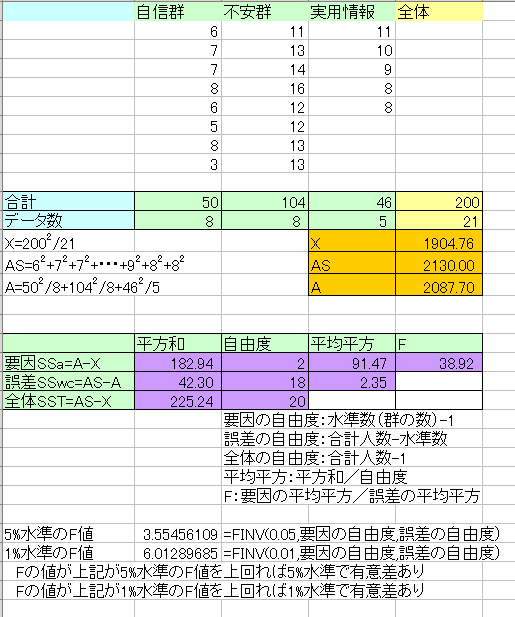
1. 各群の合計を求める（sum）
2. 各群のデータ数を求める（count）
3. Xを計算する（X=全体合計の2乗／合計人数）
4. ASを計算する（AS=個々のデータを2乗した和）（sumsq）
5. Aを計算する（A=各群の合計の2乗／各群の人数の和）
6. 平方和（要因）を計算する（A-X）
7. 平方和（誤差）を計算する（AS-A）
8. 平方和（全体）を計算する（AS-X）
9. 自由度（要因）を計算する（群の数-1）
10. 自由度（誤差）を計算する（合計人数-群の数）
11. 自由度（全体）を計算する（合計人数-1）
12. 平均平方を計算する（それぞれ平方和／自由度）
13. F値を計算する要因の平均平方／誤差の平均平方
14. 算出されたF値と5％水準のF値、1%水準のF値を比較する
15. 算出したF値>5%水準のF値なら、5%水準で有意差あり
16. 算出したF値>1%水準のF値なら、1%水準で有意差あり

多重比較

分散分析において、帰無仮説が棄却された場合、「平均値には差がある」ということになる。しかし、どの群の間で差があるのかはわからない。どの組合せで差があるのかを調べるためにはさらに多重比較を行う必要がある。

多重比較については様々な方法が提案されているが、ここでは計算が簡単なLSD法を実施する。

t値は先ほどの分散分析結果にある誤差の自由度を元に、=tinv(確率,自由度)で計算する。例えば、誤差の自由度が9で5%水準のt値を知りたい場合は=tinv(0.05,9)となり結果は2.262となる。

あとは、全てのペアについて平均値の差の絶対値を求め、LSD値と比較をしてLSD値よりも大きければ有意、小さければ有意ではないということになる。

例えば、|自信群の平均-不安群の平均|>LSD値ならば有意、<LSD値なら有意ではない。|自信群-実用情報|や|不安群-実用情報|についても確認する。

χ²検定

4-2のセキュリティの認知度は、認知している人の割合を計算している。この場合は平均値ではないので分散分析を行うことはできない。このように割合に差があるかどうかを調べるのがχ²検定である。2の個別項目の習熟率も割合を算出しているのでχ²検定を行うことが出来るが、作業量が多すぎるので今回は行わない。

χ²検定の場合も、帰無仮説をたて、この仮設を支持できる確率を計算する。今回は例えば次のような仮説が立てられる。

自信群と不安群と実用情報履修者のセキュリティの認知度の割合に差はない。

χ²検定の流れを示す。まず実際のデータを表形式にまとめ、これを観測度数とする。その上で、いずれも比率に差がないとした場合に期待される結果を期待度数としてまとめ、両者の差を調べていく。計算手順は以下の図を参照すること。

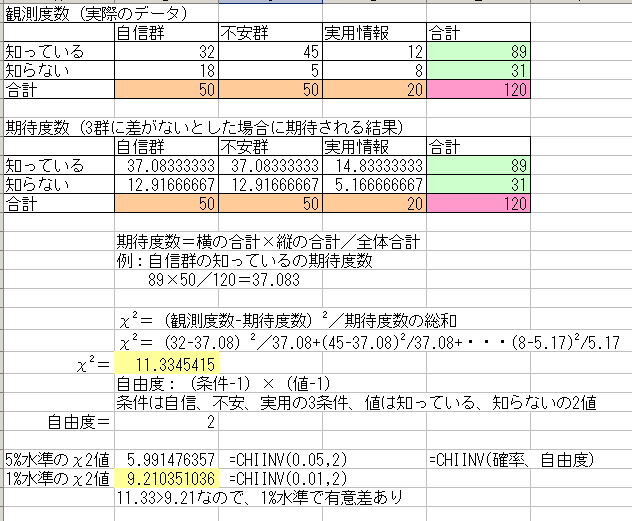
検定結果が有意であった場合、分散分析と同じように、どこに差が見られるのかを調べていく必要があるが、計算手順が複雑なのでここでは割愛する。

raw_data0622.xlsを添付ファイルで提出する。

提出要領

• To:課題提出用メールアドレス
• Subject:実用情報(13)