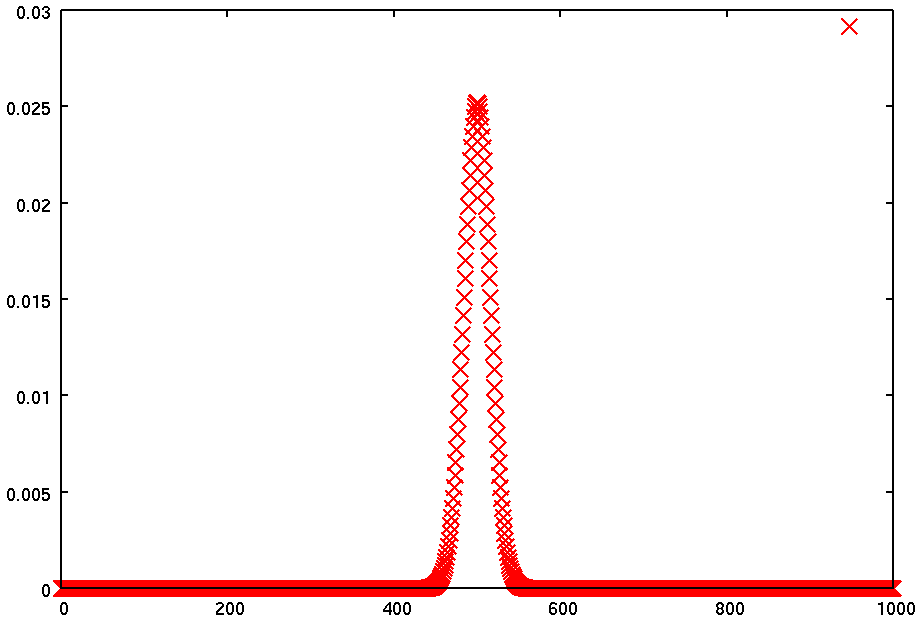
 実行すると、中央に膨らんだグラフができる。
n = 1000, p = 0.5 の場合を示した。
このプログラムによる数値計算により、
このようなデータを得る。
実行すると、中央に膨らんだグラフができる。
n = 1000, p = 0.5 の場合を示した。
このプログラムによる数値計算により、
このようなデータを得る。
実際に表と裏が同じくらい出ることを調べよう。
#!/usr/koeki/bin/ruby
def factorial(m)
if m <= 1
1
else
m × factorial(m-1)
end
end
STDERR.print("二項分布を調べます。ある事象が起きる確率を決めてください。")
p_p = gets.chomp!.to_f
if p_p > 1
exit
end
p_q = 1 - p_p
STDERR.print("標本数を決めてください。")
n = gets.chomp!.to_i
for i in 0..n
prob = factorial(n) / factorial(i) / factorial(n-i) * p_p ** (n-i) * q_p **i
#printf("%f\n",prob)
for j in 0..(prob × n).to_i
print("* *")
end
print("\n")
end
 実行すると、中央に膨らんだグラフができる。
n = 1000, p = 0.5 の場合を示した。
このプログラムによる数値計算により、
このようなデータを得る。
実行すると、中央に膨らんだグラフができる。
n = 1000, p = 0.5 の場合を示した。
このプログラムによる数値計算により、
このようなデータを得る。