二項分布と正規分布

二項分布

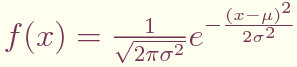
2つの事象のうちどちらかが一定の確率で出現するとき， N回の試行で各事象が何回程度現われるかの分布が二項分布である。

「コインを20回振ったときに表の出る回数を調べる」を50セット行なう

同一分布に従う独立した値の平均値の分布は正規分布に従う。つまり，元の分布がなんであるかに関らず，そこから得た複数の値の平均を取る操作を多数行なった場合，平均値の分布は正規分布となる。平均μ，標準偏差σの正規分布は

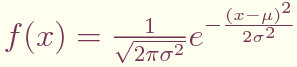
$f(x)=\frac{1}{\sqrt{2\pi\sigma^2}} e^{-\frac{(x-\mu)^2}{2\sigma^2}}$

の確率密度関数となる。特に，平均0，標準偏差1の場合の

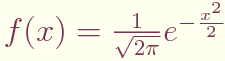
$f(x)=\frac{1}{\sqrt{2\pi}} e^{-\frac{x^2}{2}}$

で表される分布は，標準正規分布という。

yuuji

e.koeki-u.ac.jp