roy > naoya > 社会情報処理 > (5)分散分析
(5) 10/26の授業内容:分散分析
[1] 導入
カンカンラーメンと公益軒で今度は餃子対決をすることになった。すると、この対決にカフェテリアが急遽参戦し三つ巴の対決を行うことになった。駅の改札を通る人10人ごとに1人協力を求め、各店20人で計60人の協力を得、自分の食べた餃子に得点をつけることを求めた。以下がその結果である。3店の餃子の味には差があるといってようだろうか。
| カンカン | 公益軒 | カフェテリア |
| 80 | 75 | 80 |
| 75 | 70 | 80 |
| 80 | 80 | 80 |
| 90 | 85 | 90 |
| 95 | 90 | 95 |
| 80 | 75 | 85 |
| 80 | 85 | 95 |
| 85 | 80 | 90 |
| 85 | 80 | 85 |
| 80 | 75 | 90 |
| 90 | 80 | 95 |
| 80 | 75 | 85 |
| 75 | 70 | 98 |
| 90 | 85 | 95 |
| 85 | 80 | 85 |
| 85 | 75 | 85 |
| 90 | 80 | 90 |
| 90 | 80 | 90 |
| 85 | 90 | 85 |
| 80 | 80 | 85 |
[2] 3群の比較にt検定は適用できない
前回はカンカンと公益軒のカレーラーメンの味を比較するために2つの平均値の比較を行った。この際に使用したのはt検定であるが、今回は平均値が3つある。どうすれば比較をすることができるだろうか。
t検定で検討を行う場合、t検定は2つの平均値の差を検定する手法であるため以下のような組み合わせで合計3回の検定を行う必要が生じる。
- カンカン VS 公益軒
- 公益軒 VS カフェテリア
- カフェテリア VS カンカン
t検定を用いてこのように3回の検定を行うことは禁止されている。なぜだろうか。考えてみよう。
まず3つの平均値の差の検定を行う場合、以下が帰無仮説となる。
帰無仮説:3つの平均値に差はない。
この仮説が正しいのであれば、今回観察された差は偶然に生じた誤差ということになる。t検定は今回の差が偶然に発生する確率を算出するために用いている。偶然に発生する確率が5%以上であれば、偶然に発生しうると判断し帰無仮説を採択する。偶然に発生する確率が5%未満であれば、偶然に発生した差であるとはいいきれず、帰無仮説が棄却され、差がないとはいえない(=差がある)という結論が導き出される。
では3回のt検定により帰無仮説を棄却することを考えてみよう。全てが5%水準で有意であった場合、帰無仮説を棄却する水準はどれくらいになるだろうか?
- t検定(カンカン VS 公益軒):5%水準で有意=95%の確率で意味のある差
- t検定(公益軒 VS カフェテリア):5%水準で有意=95%の確率で意味のある差
- t検定(カフェテリア VS カンカン):5%水準で有意=95%の確率で意味のある差
3回の検定で帰無仮説を棄却した時の有意水準:95%×95%×95%=0.953≒0.857=85.7%の確率で意味のある差=14.3%水準で有意
結論:3つ以上の平均値について繰り返しt検定を行うと、帰無仮説を棄却する水準が不当に低くなってしまい、差が出やすくなってしまう。
[3] 分散分析の考え方
3つのお店の評価データは以下のようになっている。ここでカンカンのなかのある1つのデータについて考えてみよう。データは全体の平均からずれているが、このずれは「全体の平均とカンカンの平均のずれ」と「カンカンの平均からのズレ」に分解できる。
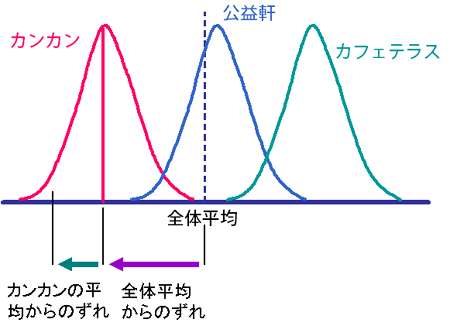
ここで「全体の平均とカンカンの平均のずれ」は全体の平均から各群(各標本集団)がどれだけずれているかをあらわしている。これを群間のズレと呼ぶ。
一方、「カンカンの平均からのずれ」は群(標本集団)の中で、個々のデータがどれだけずれているかをあらわしている。これを群内のずれとよぶ。
つまり、すべてのデータについて
全体の平均からのズレ = 群間のズレ + 群内のズレ
が成り立つ。
群内のずれは標本集団の間の違いを表している。これが大きくなるということは、各群の平均が大きく異なるということになる。一方、群内のずれは、同じ標本集団の中でのばらつきであり「誤差」や「個人差」として扱うことができる。
もし、群内のずれに比べて、群間のずれが大きければ、標本集団の間の違いが大きいということになるので、「母集団の平均に差がない」という帰無仮説を棄却することになる。逆に、群内のずれに比べて、群間のすれが小さければ、標本集団の間の差が大きいとはいえないので、「母集団の平均に差がない」という帰無仮説を採択することになる。
[4] 分散分析をしてみよう
- カンカン、公益軒、カフェテリアのデータ数を求める(count関数)
- カンカン、公益軒、カフェテリア、全体の合計を求める(sum関数)
- カンカン、公益軒、カフェテリアの平均値を求める(average関数)
- 修正項(X)を計算する(X=全体合計の2乗/(要因数×データ数)=5033^2/(3×20))
以上の計算が終わったら、分散分析表(図中下側)を作成する。

- 要因平方和:各要因の合計の2乗和/データ数-X=(1680^2+1590^2+1763^2)/20-X
- 全平方和:全データの2乗和-X=80^2+75^2+・・・85^2-X(2乗和にはsumsqという関数がある)
- 誤差平方和:全平方和−要因平方和
- 自由度(要因平方和)は群の数-1=3-1=2
- 自由度(誤差平方和)は全平方和の自由度−要因平方和の自由度=59−2=57
- 自由度(全平方和)は群の数×データ数-1=3×20-1=59
- 平均平方はいずれも平方和/自由度
- Fは平均平方(要因)/平均平方(誤差)
[5] F分布表
χ2乗検定では「χ2乗分布表」を見た。またt検定では「t分布表」を見た。分散分析でもF値が求められたら「F分布表」を見る。
F分布表を見る際には2つの自由度すなわち、群間の自由度と群内の自由度を利用する。ここでは2と57を使用する。
| 群内の自由度 | 群間の自由度 | ||||
| 1 | 2 | 3 | 4 | 5 | |
| 10 | 4.96 | 4.10 | 3.71 | 3.48 | 3.33 |
| 20 | 4.35 | 3.49 | 3.10 | 2.87 | 2.71 |
| 30 | 4.17 | 3.32 | 2.92 | 2.69 | 2.53 |
| 40 | 4.08 | 3.23 | 2.84 | 2.61 | 2.45 |
| 50 | 4.03 | 3.18 | 2.79 | 2.56 | 2.40 |
| 60 | 4.00 | 3.15 | 2.76 | 2.53 | 2.37 |
| 70 | 3.98 | 3.13 | 2.74 | 2.50 | 2.35 |
| 80 | 3.96 | 3.11 | 2.72 | 2.49 | 2.33 |
| 90 | 3.95 | 3.10 | 2.71 | 2.47 | 2.32 |
| 100 | 3.94 | 3.09 | 2.70 | 2.46 | 2.31 |
| 200 | 3.89 | 3.04 | 2.65 | 2.42 | 2.26 |
| 300 | 3.87 | 3.03 | 2.63 | 2.40 | 2.24 |
この表には群内57に該当する値がないので、最も近い60のところを見る。そうすると、F=3.15よりも大きな値であれば5%水準で有意となることがわかる。
今計算で求めたFはこの値よりも大きいため、5%水準で棄却域に入る。これにより帰無仮説である「3つのお店の餃子の評価の平均に差はない」は棄却され、「3つのお店の餃子の評価の平均には差がある」ことになる。
なお、F分布表に記載がない自由度における1%水準、5%水準で有意となるF値は表計算ソフトにより以下の関数で調べることができる。
=FINV(確率,自由度1,自由度2)
ここで5%水準の場合確率は0.05、1%水準の場合は0.01となる
[6] 多重比較
分散分析は帰無仮説の採択および棄却の判定をすることができる。しかし、棄却された場合、3つのお店の平均値には差があることがわかるのみで、どのお店とどのお店に差があるのかまではわからない。どの組み合わせで差があるのかを調べるためにはさらに多重比較を実施しなければならない。
多重比較については様々な方法が提案されているが、ここでは比較的利用されることが多いライアン法について簡単に説明する。
ライアン法は全てのペアについてt検定を実施する多重比較法である。ただし、有意水準5%のままで検定を実施すると上述の通り問題があるため、有意水準を調整する。
また、t検定を実施する順番も規定されている。群が3つの場合は説明しづらい(簡単だが応用しづらい)ので店A、店B、店C、店Dの4つで分散分析の結果が有意である場合を例に説明をする。ここで平均値は店A>店B>店C>店Dとし、大きい順にデータを並べているものとする。
- 最大値(店A)と最小値(店D)でt検定をする。有意でない場合はこれで終了。有意である場合は2に進む。
- 1は最大値と最小値の距離が4(自分自身を含む)。次の段階では距離が3の全てのペアを対象にt検定を行う。1つも有意なものがなければ終了。1つでも有意であれば3に進む。
- 距離が2の全てのペアについてt検定を行う。
t検定を行う場合、t値を求める方法は前回の授業で行ったとおりであるが、有意であるかどうかの判定はt分布表ではなく、以下に従う。
まず有意水準を求める。有意水準はt検定を行うペアの距離により異なり、以下の式による。
有意水準=2α/m(r-1)
ここで、α:分散分析の有意水準(0.05or0.01)、m:群の数、r:比較したいペアの距離
有意水準は5%や1%よりも小さな値になる。この値に対応するt値は以下の式で求める。
tの臨界値=zα+((z3α+zα)/4×(自由度-2))
ここで、zα:上で求めた有意水準に対応するz値、自由度:全データ数-群数
各ペアについてt検定を実施し、上で求めたtの臨界値よりも大きければαで指定した水準(5%もしくは1%)で有意となる。
[7] レポート課題
最後に3つのお店の普通のラーメンの味の評価に差があるかどうか調べてみよう。
| カンカン | 公益軒 | カフェテラス |
| 90 | 75 | 65 |
| 70 | 95 | 60 |
| 75 | 75 | 75 |
| 90 | 80 | 80 |
| 65 | 75 | 65 |
| 70 | 85 | 60 |
| 80 | 75 | 70 |
| 85 | 85 | 85 |
| 75 | 80 | 70 |
| 75 | 65 | 75 |
| 85 | 90 | 75 |
| 75 | 75 | 70 |
| 80 | 90 | 80 |
| 90 | 75 | 75 |
| 80 | 85 | 80 |
この問題について、新規にエクセルファイルを作成しanova.xlsと同一の手順で分析を進め、結果がどうなるか確認し、結論をワークシートの余白に記載する。
提出要領
- To: naoya @ e.koeki-u.ac.jp(@前後のスペースを除去すること)
- Subject: 社会情報処理(5)
- 提出期限:次回授業開始時まで
- ファイルを添付して送ること。ファイル名は学籍番号-shakai5.xls