roy > naoya > 基礎プログラミングII[月2] > (8)再帰
(8) 12/01の授業内容:再帰
再帰とは
前回の授業では、def-endを用いてメソッドを定義する方法について学んだ。プログラムの中で繰り返し使用する処理をメソッドとして独立させておくと、毎回呼び出せばよいことになり、同じことを何度も書く必要がなくなるというメリットがあった。今日は、メソッドが自分自身を呼び出すという特殊な用法について学ぶ。メソッドが自分自身を再度呼び出すことを再帰呼び出しと呼ぶ。
1つ例を挙げよう。以下の図は10進数XをY進数に変換する手続きを示したものである。これまでは10進数を2進数に変換する方法のみを取り上げてきたが、同じ方法で、6進数や9進数に変換することもできる。
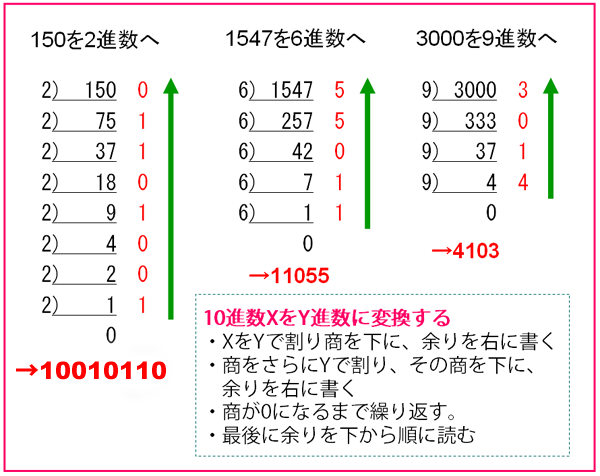
今回取り上げるのは2進数のみとするため、左端の10進数150を2進数に変換する手続きのみを確認する。2進数に変換するためには2で割り続け、商を下に書き、余りを右に書く。これを延々と繰り返し、商が0になった時点で右側に書かれた余りを下から上に向かって読むと、2進数に変換した結果となる。
ここで、10進数の150を2進数に変換する手続きを以下のように言うことも出来る。
10進数150の2進数への変換
10進数75を2進数に変換した結果の末尾に「0」をつけたものである。
※150を2で割った余りが0であるため、上の定義では「0」としている。150を2で割った余りは150%2と標記できるので、以下のように書いても同じことである。
10進数75を2進数に変換した結果の末尾に150%2をつけたものである。
75を2進数に変換した結果は「1001011」であるから、150を2進数にするためには、末尾に150%2の結果である「0」を追加して、「10010110」となる。では、10進数75を2進数に変換するためにはどうしたらよいだろうか。これは次のように定義をすることができる。
10進数75の2進数への変換
10進数37を2進数に変換した結果の末尾に75%2をつけたものである。
登場する数字は異なるが、定義自体は150の場合と同様である。同じように37を2進数に変換する場合も
10進数37の2進数への変換
10進数18を2進数に変換した結果の末尾に37%2をつけたものである。
となる。同じ定義が延々と繰り返されるわけである。プログラムの中で同じ処理を繰り返し行う場合は、def-endでメソッドを作って呼び出すのが効率的であることから、これについてもメソッドを作成することが考えられる。
しかし、10進数150を2進数に変換するためのメソッドを作っている最中であるとすれば、そのメソッドが行う処理の内容を書いている途中で、再度そのメソッドを呼び出さなければならないと言うことになる。これが、再帰呼び出しである。
ちなみに、これまでの定義では150とか37というような具体的な数字を入れ込んでいたが、これをもう少し一般化してみよう。
10進数150の2進数への変換
10進数75を2進数に変換した結果の末尾に150%2をつけたものである。
10進数75の2進数への変換
10進数37を2進数に変換した結果の末尾に75%2をつけたものである。
これらの数字に着目すると、150と75の関係、75と37の関係はいずれも150/2=75、75/2=37というように2で割った値であることがわかる(整数なので小数点以下は切捨てとなるので75/2=37が成り立つ)。したがって、10進数nを2進数に変換するための定義は次のように書くことができる。
10進数nの2進数への変換
10進数n/2を2進数に変換した結果の末尾にn%2をつけたものである。
nを使えば、これまで延々と書いてきた定義を、1つの定義で済ませることができる。ただし、これだけでは定義としては不十分である。進数変換は商が0になった時点で終了というストップルールがある。割られる数<割る数の場合に商が0となるので、この条件を組み込めば上の定義は次のように書き直すことができる。
10進数nの2進数への変換
10進数n/2を2進数に変換した結果の末尾にn%2をつけたものである。ただし、n<2の場合は変換結果はn%2となる。
2進数への変換の場合は割る数は常に「2」なので、n<2としている。n<2であれば必ず商は0になるので、この時のn%2の値が変換した2進数の先頭の値になる。
10進数→2進数への変換を再帰呼び出しを用いて書く
では、上で作成した定義に基づいてプログラムを作成してみよう。
#!usr/koeki/bin/ruby
def henkan(n)
if n < 2
n%2
else
sho = n/2
amari = n%2
henkan(sho).to_s + amari.to_s
end
end
STDERR.print "10進数を入力(2進数に変換します):"
datum = gets.chomp!.to_i
printf("%dを2進数に変換すると%dです。\n",datum, henkan(datum))
プログラムを実行するとdef-endの下から処理が始まり、10進数の入力が促される。これをdatumに代入し、最終行のhenkan(datum)でhenkanメソッドを呼び出している。
henkanメソッドはif文を用いた分岐が行なわれており、if側は2で割り付けた際の最後の1回の処理の時のみ使われる(ストップルール)。これは、先ほどの定義のうち、「ただし、n<2の場合は変換結果はn%2となる」の部分に相当する。
else側がそれ以外の場合で、2で割った値をshoに、2で割った余りをamariに代入した上で、henkan(sho).to_s + amari.to_s としている。これは、定義の中の「10進数n/2を2進数に変換した結果の末尾にn%2をつけたものである。」の部分を書いたものである。n/2を2進数に変換した結果は既知ではないので、henkan(sho)として、再度メソッドを呼び出している。なお、余りを末尾に追加するにあたり、仮にhenkan(sho)+amariとすると数字の足し算となるため、たとえば1+1は11にならず2になってしまう。これを避けるため.to_sメソッドをつけて文字列に変換している。
再起呼び出しのポイント
- 問題を分割して考えたときに、分割した部分を解く方法と、全体を解く方法が同じである場合、再帰を使うことができる
- 問題分割を繰り返し、これ以上問題が分割できない場合に結果そを返す条件を入れる
- 分割した問題を再帰的に同じメソッドを呼んで得られた結果を合成したものを最後の結果として返す
出席課題
10進数を2進数に変換するプログラムをみてきたが、6進数や9進数への変換も同様の手続きで行なうことが出来る。これを踏まえた上で、次の1番、2番を実施しなさい。難しいと感じる場合は1番のみでも構わない。
- 10進数XのY進数への変換について再帰的な定義をせよ。定義を文章で書けばよい。
- 10進数を2進数に変換するプログラムを書き換え、10進数を2〜9進数に変換できるようにせよ。実行時に元の10進数に加え、何進数に変換したいか(ただし、2〜9進数に限定)を入力させ、この2つの値を使ってhenkanメソッドを呼び出せばよい。
制限時間は15分。出席点は2点。提出要領は下記の通り。
- 提出先:課題提出用メールアドレス
- メールのSubject:attend08
- 本文の構成:1行目で学籍番号、氏名を記載する。2行目以降に解答を記載する。
Tips:emacsでの日本語入力のオンオフはCtrl-oです
Tips:Mewによるメールの送り方はMewコマンドを参照
再帰を利用したプログラミング[1]
1からNまでの足し算
1からNまでの足し算を例に挙げ、再帰について考えてみよう。
例えば、5までの足し算の場合、1+2+3+4+5とか5+4+3+2+1と書く。Nまでの足し算の場合はN+(N-1)+(N-2)+...+2+1となる。
再帰的な方法で1からNの足し算の計算方法を定義してみよう。
1からNまでの足し算の再帰的定義
1からNまでの足し算とは、1からN-1まで足した結果にNを加えたものである。ただし、Nが1の場合は1である。
これをプログラムで書くと下記の通りになる(recursive-sum.rb)
#!/usr/koeki/bin/ruby/
def sum(n)
if n == 1
1
else
n + sum(n-1)
end
end
STDERR.print"好きな数字を入力してください"
number = gets.chomp!.to_i
printf("1から%dまで足すと%dになります。\n",number,sum(number))
問題となるのはdef-endの定義内容である。特に下記の行に着目しよう。
n + sum(n-1)
sumというメソッドの定義の中で、再度sumが呼び出されている。
number=4とした場合の、このプログラムの動きを確認してみよう
- sum(4)が呼び出される
- sum(4)=4+sum(4-1)なのでsum(3)が呼び出される
- sum(3)=3+sum(3-1)なのでsum(2)が呼び出される
- sum(2)=2+sum(2-1)なのでsum(1)が呼び出される
- sum(1)=1なのでsum(1)として1が返される
- sum(2)=2+sum(1)なのでsum(2)として3が返される
- sum(3)=3+sum(2)なのでsum(3)として6が返される
- sum(4)=4+sum(3)なのでsum(4)として10が返される
- 「1から4まで足すと10になります」と表示される
再帰を利用したプログラミング[2]
階乗の計算
階乗の計算を使って、再起についてもう少し考えてみよう。
階乗の計算とは n! で表記され n!=n*(n-1)*(n-2)*・・・2*1で表現される。例えば5の階乗であれば、5!=5*4*3*2*1となる。
再帰的な方法で階乗の計算の方法を定義してみよう。
階乗計算の再帰的定義
Nの階乗とは N-1の階乗とNを掛けたものである。ただし、1の階乗は1である
これをプログラムで書くと下記の通りになる(factorial.rb)
#!/usr/koeki/bin/ruby/
def factorial(n)
if n <= 1
1
else
n * factorial(n-1)
end
end
STDERR.print"好きな数字を入力してください"
number = gets.chomp!.to_i
printf("%dの階乗は%dです\n",number,factorial(number))
問題となるのはdef-endの定義内容である。特に下記の行に着目しよう。
n * factorial(n-1)
factorialというメソッドの定義の中で、再度factorialが呼び出されている。
number=4とした場合の、このプログラムの動きを確認してみよう
- factorial(4)が呼び出される
- factorial(4)=4*factorial(4-1)なのでfactorial(3)が呼び出される
- factorial(3)=3*factorial(3-1)なのでfactorial(2)が呼び出される
- factorial(2)=2*factorial(2-1)なのでfactorial(1)が呼び出される
- factorial(1)=1なのでfactorial(1)として1が返される
- factorial(2)=2*factorial(1)なのでfactorial(2)として2が返される
- factorial(3)=3*factorial(2)なのでfactorial(3)として6が返される
- factorial(4)=4*factorial(3)なのでfactorial(4)として24が返される
- 「4の階乗は24です」と表示される
プログラムの流れは上記の通りである。階乗の計算は比較的単純であるため、こんな複雑なことをしなくてもプログラムを書くことができそうな気がする。しかし、再帰的な方法は、複雑な処理を繰り返し行う場合には大きな力を発揮する。
再帰を用いたソート
大小関係が定められたデータを、大きい順(降順)や小さい順(昇順)に並べ替える作業をソートという。Rubyにはsortメソッドが備わっており、ソート自体を実行するプログラムを書く必要はない。しかし、実際にはソートは奥の深いテーマであり、いかに効率的に実行するかという観点より様々な方法が提案されている。
クイックソート
n個の要素から任意の要素aを取り出す。残りの要素についてaよりも大きければ右側、小さければ左側に配置する。先頭の要素を基準として左右に振り分ける作業をクイックソートと呼ぶ。クイックソートを繰り返すことで、左右に振り分けられる値が0個もしくは1個となる。この時点で並び替えは終了となる。
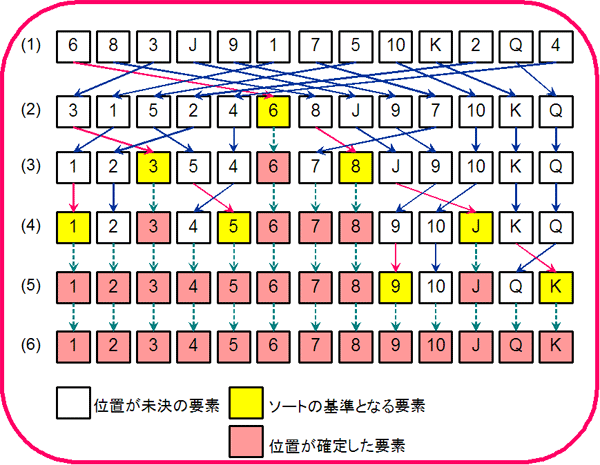
この図では最初に先頭の要素である6を取り出している。そして6を基準として、6よりも大きければ右側に配置し、小さければ左側に配置している。次に左右に配置された要素について、それぞれ先頭(左は3、右は8)を基準として同様にクイックソートを行っている。
2回目のクイックソートを行った時点で、8の左側の山は値が「7」の1つのみとなっている。1つの場合はこれ以上の並び替えはできないため、これで順番が確定になる。3の左右、8の右側についてクイックソートを継続する。
3回目のクイックソートを行うと左から2つの山については順番が確定となる。一番右側の山のみまだ順番が確定していない。
一番右側の山について4回目のクイックソートを実行する。これですべての順番が確定する。
これをプログラムで書くと下記のとおりになる(quicksort.rb)。
#!/usr/koeki/bin/ruby def quicksort(data) # 配列(順番がばらばらなデータ)を受け取る if data.length <= 1 # データが1個以下なら data # そのものを返して並べ換え完了 else left = [] # left(左側配列)を新規作成 left = Array.new でも可 right = [] # right(右側配列)を新規作成 right = Array.new でも可 k = data.shift # 配列dataの先頭を取り出してkにする(破壊的操作) for x in data # 残ったdata全てに対して繰り返す if x < k # kより小さかったら left << x # 左側に追加(<<は配列末尾への破壊的要素追加、pushと同じ) else right << x # 右側に追加(同上) end # ifに対するend end # forに対するend quicksort(left) + [k] + quicksort(right) # quicksort(left) と k と quicksort(right) を合体したものが最終結果 # kは要素なので[]で括って配列にする end # ifに対するend end # defに対するend def ketsugo(a) # 配列を受け取ってjoinメソッドで結合して返す printf("[%s]\n", a.join(", ")) end # defに対するend array = [] while true # 配列に好きな数値を順次代入 STDERR.print"好きな数字を入力(終了はq)" datum = gets.chomp! if datum == "q" then break end array.push(datum.to_i) # pushで配列arrayの末尾に追加(<<でも同じ) end print"もとの順番\n" ketsugo(array) # ketsugoメソッドの呼び出し print"並べ替え後\n" ketsugo(quicksort(array)) # ketsugoメソッドの呼び出し # 引数はquicksortを呼び出した結果
pan{c10xxxx}% ruby quick_sort.rb[Return]
好きな数字を入力(終了はq)400
好きな数字を入力(終了はq)204
好きな数字を入力(終了はq)346
好きな数字を入力(終了はq)958
好きな数字を入力(終了はq)225
好きな数字を入力(終了はq)367
好きな数字を入力(終了はq)784
好きな数字を入力(終了はq)q
もとの順番
[400,204,346,958,225,367,784]
並べ替え後
[204,225,346,367,400,784,958]
その他のソート バブルソート
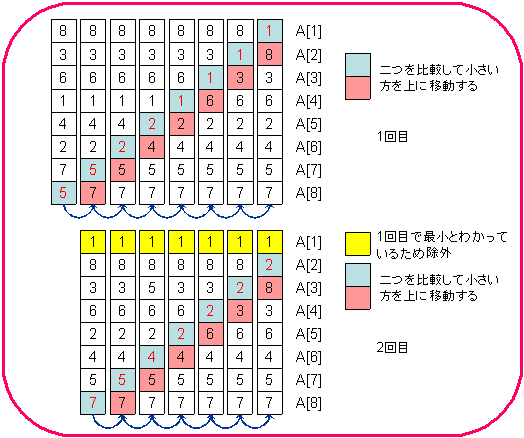
n個の要素を想定した場合に、一番最後の値であるA[n]を基準として、A[n-1]、A[n-2]、...と大小比較をしていく。添え字が小さいほうに小さい値が保持されるようにする。例えばA[n]とA[n-1]の大小比較を行った場合、A[n-1]の方が小さければそのまま、A[n]の方が小さければA[n]とA[n-1]を入れ替え、A[n-1]に小さい値が入るようにする。次にA[n-1]とA[n-2]の大小比較をする。今度はA[n-2]に小さい値が入るようにする。これを順番に繰り返しながら先頭のA[1]まで比較を行う。これにより最も小さい値がA[1]に入る。
A[1]に最も小さい値が入ったら、2回目はA[n]から開始してA[2]まで大小比較を行う。2回目の大小比較を行った結果としてA[2]に2番目に小さい値が入ることになる。これを繰り返すことで、最終的に小さい順の並び替えが完了する。
レポート課題
以下のうちいずれかを選んで解答する。
問題1(8点満点):これまでに作成したプログラムの中から1つを選び、自分のWebページで公開する。htmlの文法の正しさに基づき採点する。なお作成するのはhtmlファイル1つであり、その中にプログラムの概要とプログラムを記載する。デザインや概要の文章を工夫して、プログラムを実行してみたくなるようなページ作りを心がける。なお、htmlファイル作成にあたってはtext-decorationやline-heightなどのCSSのプロパティを最低でも6種類は使用すること。
問題2(8点満点):問3を再帰を使わずに書く。def-endも使用しなくても良い。
問題3(10点満点):バブルソートを再帰を用いて書く。
- 提出先:課題提出用メールアドレス
- 提出期限:12/14(日)23:00
- メールのSubject:課題6
- 本文の構成:1行目で学籍番号、氏名を記載する。2行目以降は下記の構成とする
問題1の場合
- プログラムを掲載したWebページのURL
- 感想
問題2、3の場合
- 作成したプログラム
- プログラムの実行結果
- プログラムの説明
- 感想
- 採点基準(問題1):期限内提出点(2点)、メールの体裁(1点)、CSS・デザイン(2点)、htmlの構文(3点):htmlの構文はAnother HTML-lint gatewayで採点し、マイナスなら0点、50点以下なら1点、100点未満なら2点、100点なら3点とする。
- 採点基準(問題2、3):期限内提出点(2点)、メールの体裁(1点)、プログラム(2〜4点)、プログラムの説明(3点)
- プログラムの説明:問題2は進数計算をプログラムでどのように実装したかについて、問題3は再帰処理を行っている部分について、処理の流れを追いながら詳しく説明する。
- わかりにくい説明や、Webページを単にコピー&ペーストしただけの説明は減点することがある。一度読み直してから提出すること。
- 驚異的に良くできているレポートについては満点を超える得点をつけることがある。
- よくできていたレポートは、他の人の参考になるよう、本人が特定できないような形で掲載する。掲載してほしくない場合はメールでの課題提出時にその旨記載すること。
Tips:emacsでの日本語入力のオンオフはCtrl-oです
Tips:ktermでのプログラムの実行結果をメールに貼り付けるには、コピーしたい箇所をマウスで選択し、emacs(Mew)上でマウスの真ん中ボタンをクリックする
Tips:Mewによるメールの送り方はMewコマンドを参照