gnuplot は GPL ライセンスのグラフ作成ソフトである。
% gnuplot
として kterm 内で作業する。
> plot sin(x)
とすると、グラフが現れる。ベキは ** で表す。
x**2 を描いてみよう。
気に入ったグラフができたら、
> save "グラフ.plt"
で保存する。
以前描いたグラフを呼び出すには、
> load "グラフ.plt"
とする。
グラフを複数書きこむためには
> plot 関数 1, 関数 2
と , でつなぐ。
> set terminal postscript
したあとに、
> set output "グラフ.ps"
として PS ファイルに変換して出力させることができる。
> set terminal png > set outout "グラフ.png" > replot
で png ファイル型式に変換される。
実験データは、あらかじめどこかに入力しておく。 ここでは 米国 MIT、スウェーデンのウプサラ大学、筑波の KEK の計算機からの返事の速さを測定したデータで調べてみよう。
このようにして、3 つの場所について 3 回時間を変えて測定した。 それぞれ、{mit,uu,kek}i.txt (i=1,2,3), とする。 平均や標準偏差を求めるプログラムは readdata.rb とした。
それぞれの平均と標準偏差を求めたデータはこのようにまとまった。
### mit 17 213.388 4.601 ### mit 16 218.687 8.254 ### mit 20 214.967 4.795 ### uu 18 335.554 6.975 ### uu 21 331.614 3.197 ### uu 17 336.369 6.889 ### kek 14 26.810 5.563 ### kek 18 31.252 8.441 ### kek 21 30.690 8.379
次に、緯度から移動距離を計算してみよう。地球は球面なので、 球面上の距離の計算を行う。 本学(38.89N, 139.82E) から、 KEK(36.15N, 140.07) までは 360.5 km、 ウプサラ大学(59.53N, 17.38E) までは 7,801.7 km、 MIT(42:21N, 71:05W) までは 10,390.3 km と計算される。
これらのデータを使って、距離と接続の速さとに関係があるのかどうか、 グラフ化して調べてみよう。
コメントは # である。dtd10data.dat とする。
# MIT 10390.3 213.388 4.601 10390.3 218.687 8.254 10390.3 214.967 4.795 # UU 7801.7 335.554 6.975 7801.7 331.614 3.197 7801.7 336.369 6.889 # KEK 360.5 26.810 5.563 360.5 31.252 8.441 360.5 30.690 8.379
命令は、kterm で gnuplot を立ち上げ、
gnuplot> plot "dtd_gnuplot_data.dat" index 0:0 using 1:2:3 with yerrorbars, \ > "dtd_gnuplot_data.dat" index 1:1 using 1:2:3 with yerrorbars, \ > "dtd_gnuplot_data.dat" index 2:2 using 1:2:3 with yerrorbars
とする。1:2:3 は、データを右端から 1, 2, 3 と振り、横軸、縦軸、誤差とし、 データのブロックは 0:0, 1:1, 2:2 と表す。
データの名前をはっきりさせたいので、データを明示するには、
gnuplot> plot "dtd_gnuplot_data.dat" index 0:0 using 1:2:3 title "MIT" with yerrorbars, \ > "dtd_gnuplot_data.dat" index 1:1 using 1:2:3 title "UU" with yerrorbars, \ > "dtd_gnuplot_data.dat" index 2:2 using 1:2:3 title "KEK" with yerrorbars
軸の名前を明示するには
gnuplot> set xlabel "Distance [km]" gnuplot> set ylabel "Connection Speed [ms]" gnuplot> replot
とする。他のところも調べてみたらよいが、この 3 個所からの測定では、 接続の速さと地理的な距離には相関がなさそうであるし、 速さにばらつきはほとんど見られないようである。
gnuplot> set term tgif Terminal type set to 'tgif' Options are 'portrait [1,1] dashed "Helvetica" 18' gnuplot> set output "保存したいファイル名.obj" gnuplot> replot gnuplot> save "保存したいファイル名.plt" gnuplot> quit
直接 gs ファイルなどでもよいが、白黒になってしまうので、 カラーで保存したければ、tgif ファイルにしたあと、 tgif を使って保存するとよい。
円周率を求めるのに 2 次元配列として、 ふったサイコロの組み合わせを座標として求めるプログラムで 実行状態を再現するグラフを書いてみよう。
最小自乗法には fit を用いる。 最初に乗るべき関数を定義したあと、パラメータを計算させる。
> plot "planet081104_dat" > f(x) = a * sin(x) + b * cos(x) + c
使ったデータはこれ
> fit f(x) "planet081104_dat.dat" via a, b, c
Iteration 0
WSSR : 1.09142e+19 delta(WSSR)/WSSR : 0
delta(WSSR) : 0 limit for stopping : 1e-05
lambda : 0.816497
initial set of free parameter values
a = 1.66317e+09
b = -2.15942e+08
c = 5.04586e+08
**/
Iteration 1
WSSR : 1.09142e+19 delta(WSSR)/WSSR : -3.7529e-16
delta(WSSR) : -4096 limit for stopping : 1e-05
lambda : 8.16497
resultant parameter values
a = 1.66317e+09
b = -2.15942e+08
c = 5.04586e+08
After 1 iterations the fit converged.
final sum of squares of residuals : 1.09142e+19
rel. change during last iteration : -3.7529e-16
degrees of freedom (ndf) : 6
rms of residuals (stdfit) = sqrt(WSSR/ndf) : 1.34872e+09
variance of residuals (reduced chisquare) = WSSR/ndf : 1.81904e+18
Final set of parameters Asymptotic Standard Error
======================= ==========================
a = 1.66317e+09 +/- 6.271e+08 (37.71%)
b = -2.15942e+08 +/- 7.384e+08 (341.9%)
c = 5.04586e+08 +/- 5.132e+08 (101.7%)
correlation matrix of the fit parameters:
a b c
a 1.000
b -0.070 1.000
c 0.114 -0.475 1.000
最小自乗法のパラメータを計算したあとに
> replot f(x)
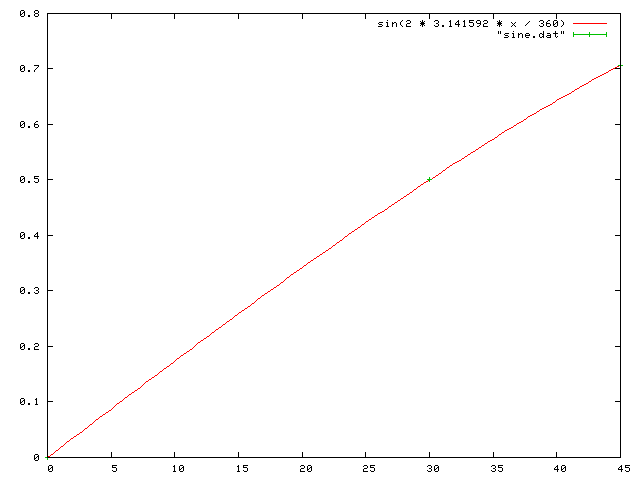
正弦関数を小数値に計算したものをしまうプログラム。 実行結果と、これを gnuplot で グラフにのせる作業例は以下の通り。
gnuplot> plot sin(pi * x / 180) with lines, "sine.dat" with yerr
ある年の得点データの分布がこのようだったとする。
Terminal type set to 'x11' gnuplot> set boxwidth 1 gnuplot> plot [0:100][0:10] "bar.txt" with boxes gnuplot> set term png Terminal type set to 'png' Options are 'small color picsize 640 480 ' gnuplot> set output "bar.png" gnuplot> replot gnuplot> save "bar.plt" gnuplot> quit
最後は念のために Gnuplot 形式で保存した。 グラフは次のようになる。

振幅は、中心の位置からどれだけ離れたかという距離を測ったもの。 ある方向を正ととると、 同じ距離だけ離れて反対側にある場合は負ということができる。
前回までに作った度数表で、半径 1 とした場合の振幅を調べよ。 またそれは何を調べることに計算できるか。
Ruby 言語で、module を使い、Math::sin(x) で調べよ。
弧度法と度数を表にした一覧を、 出力するプログラム dtd_radian.rb が radian.csv として、CSV 形式で値を出力するように作成せよ。
ruby+gnuplot が使える。
#!/usr/koeki/bin/ruby
#coding: euc-jp
require 'gnuplot'
Gnuplot.open do |gp|
Gnuplot::Plot.new( gp ) do |plot|
plot.title "Array Plot Example"
plot.ylabel "x"
plot.xlabel "x^2"
x = (0..50).collect { |v| v.to_f }
y = x.collect { |v| v ** 2 }
plot.data << Gnuplot::DataSet.new( [x, y] ) do |ds|
ds.with = "linespoints"
ds.notitle
end
end
end
#!/usr/koeki/bin/ruby
# -*- coding: euc-jp -*-
require 'gnuplot'
Gnuplot.open do |gp|
Gnuplot::Plot.new( gp ) do |plot|
plot.xrange "[-10:10]"
plot.title "Sin Wave Example"
plot.ylabel "x"
plot.xlabel "sin(x)"
plot.data << Gnuplot::DataSet.new( "sin(x)" ) do |ds|
ds.with = "lines"
ds.linewidth = 4
end
end
#sleep 10
end
#!/usr/koeki/bin/ruby
# -*- coding: euc-jp -*-
require 'gnuplot'
Gnuplot.open do |gp|
File.open( "gnuplot.dat", "w") do |gp|
Gnuplot::Plot.new( gp ) do |plot|
plot.xrange "[-10:10]"
plot.title "Sin Wave Example"
plot.ylabel "x"
plot.xlabel "sin(x)"
x = (0..50).collect { |v| v.to_f }
y = x.collect { |v| v ** 2 }
plot.data = [
Gnuplot::DataSet.new( "sin(x)" ) { |ds|
ds.with = "lines"
ds.title = "String function"
ds.linewidth = 4
},
Gnuplot::DataSet.new( [x, y] ) { |ds|
ds.with = "linespoints"
ds.title = "Array data"
}
]
end
end
#!/usr/koeki/bin/ruby
# -*- coding: euc-jp -*-
require 'gnuplot'
Gnuplot::SPlot.new( gp ) do |plot|
plot.xrange "[-10:10]"
plot.yrange "[-10:10]"
plot.title "Example"
plot.ylabel "y"
plot.xlabel "x"
plot.zlabel "z"
x_dots = Range.new(-10, 10).to_a
y_dots = Range.new(-10, 10).to_a
data = Array.new
z = Array.new
x_dots.each_with_index do |x, i|
z[i] = Array.new
y_dots.each_with_index do |y, j|
z[i][j] = x ** 2 + y ** 2
end
end
data = [x_dots, y_dots, z]
plot.data << Gnuplot::DataSet.new( data ) do |ds|
ds.with = "points"
end
end
end
濃度算の求めかたのパターンをもとめ、 ランダムに内容物を変えて、問題を出せるようなプログラムを考えてみよう。