確率分布の例

確率分布にはいくつか例がある。二項分布や、Poisson 分布、 正規分布などである。

これらは、連続極限などを取ると、互いに関係がつく。

• 二項分布: 確率分布が 2 項のもの。
• Poisson 分布: 確率分布が 0 から無限大の階級で、無限大の回数起こりうる事象を扱う。
• 正規分布: 二項分布や Poisson 分布の局限。 平均値が最も起こると考えたときの分布。 確率分布の範囲は-∞ から ∞ 全ての階級で起こると考える。 (くわしくは次週)

Poisson 分布

lim _{n → ∞} (1 - λ/n)ⁿ = e ^-λ を使うと、平均が λ/n である二項分布が多数回 n 発生したときの極限 となる。

lim _{n → ∞ n}C_k p^k(1-p)^n-k = n/n (n-1)/n (n-2)/n ...(n-k+1)/n λ^k/k! (1-λ/n)ⁿ(1-λ/n)^-k = λ^k / k! e ^-λ

例としては、交差点を通過する車両の台数、Trr の入力間違いの回数、 などがある。

期待値、分散ともに λ となる。

n = 100, λ = 10 のときの結果。n が十分大きく、λ が 5 より大きくなると、正規分布に近づく。

正規分布と標準偏差

いったい標準偏差は何を知るためのものだろうか。

統計を取ると、もっとも高いピークのところが出てくる。 どのくらい確からしいかを知る目安ものを信頼区間という。 信頼区間は百分率で表す。「何パーセント信頼区間」などという。 これを標準偏差 σを用いて 表す。 正規分布では、μ ±3 σ が 「99.7% 信頼区間」である。

Chebyshev の不等式

確率変数 X の平均を m 標準偏差を σ としたとき、 任意の正の数 k に対して次の不等式が成り立つ。

P(|X-m| < k σ) ≥ 1 - 1/k²

二項分布 B(n, p)

コイントスのように、2 種類の事象を連続して試行する場合、 その分布は二項分布に従う。 n 回試行したとする。確率分布表で、X が表が出る回数、 P がその確率を表すとき、

ただし、0 < p < 1, q = 1 - p である。

Pascal の三角形から、例えば n = 6 のときの表を作成 し、実際に Combination _nC_k で計算した場合と同じものが得られることを示せ。

二項分布の平均値、分散、標準偏差

確率変数 X が、二項分布 B(n, p) に従うとき、 q = 1 - p ならば、 X の平均値 E(X), 分散 V(X), 標準偏差 σ(X) がそれぞれ 以下のように与えられる。

E(X) = np,
V(X) = npq,
σ(X) = √ (npq)

(発展)二項分布の詳しい説明

ある事柄において、 必ず 2 つの結果しか起こらない場合、それは二項分布に従う。 発見した数学者の名前から Bernoulli [べるぬーい] 分布とも呼ばれる。

例えば、コイントスを 1 回行ったとき、 表または裏が出る確率 p, q はそれぞれ 1/2 である。

コイントスを n 回行ったとき (この段落では簡単のため n を偶数と仮定して話をすすめる) 、 表 (裏) が出続ける回数がどのように分布するか、考えよう。 一番多く出現するであろうパターンは、 n / 2 回ずつ表と裏が計測される場合である。 しかしながら、実際行ってみると、全て表 (裏) が出ることもある。 今、表が出つづける確率を考える。表の出る回数を n_p とする。 (確率 P(n_p,n_q) において、n_p + n_q = n である)

一般には、

全体で n 回のトスを通じて、 ある 1 回を除いて表が出た (1 回だけ裏が出た) 場合は、

一般には、

ただし今の場合

である。全体で n 回のトスを通じて k 回裏が出た場合は結局次のようになる。

n 回のトスを通じて、 表裏の出る組み合わせを全て考えると、

となる。

二項分布の特徴

標本数 n で、ある確率が p (起こらない確率は q = 1 - p ) の二項分布は B(n,p) と表す。

平均 μ = np
分散 σ² = npq

(発展)ベルヌーイの試行 Bernoulli Trial

実際に表と裏が同じくらい出ることを調べよう。

#!/usr/koeki/bin/ruby

def factorial(m)	

if m <= 1		

1			

else			

m × factorial(m-1)	

end

end

STDERR.print("二項分布を調べます。ある事象が起きる確率を決めてください。")

p_p = gets.chomp!.to_f

if p_p > 1 

exit

end

p_q = 1 - p_p

STDERR.print("標本数を決めてください。")

n = gets.chomp!.to_i

for i in 0..n

prob = factorial(n) / factorial(i) / factorial(n-i) * p_p ** (n-i) * q_p **i

#printf("%f\n",prob)

for j in 0..(prob × n).to_i 

print("* *")

end

print("\n")

end

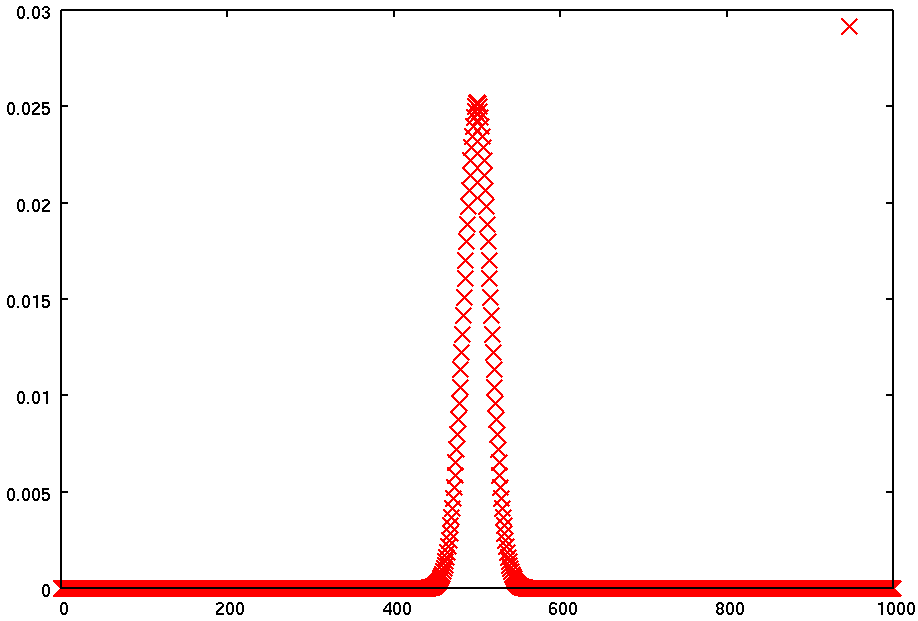実行すると、中央に膨らんだグラフができる。 n = 1000, p = 0.5 の場合を示した。 このプログラムによる数値計算により、 このようなデータを得る。