統計の用語
統計の用語についてまとめる。
- 母集団 (population)
- 調査したデータの集団のこと。
- 全体調査
- データの全てを取った場合
- 標本 (sample)
- 標本調査
- 一部を取り出し、標本でデータの特性値を調べる方法。
データの分布特性を表す概念
標本分布の特性値についてまとめる。
ある集合の要素を小さい順に書き、これを A = {0, 0, 1, 2, 3, 6} とする。
- 平均値 (average)
- 全ての値の和をデータの個数で割ったもの: (0 + 0 + 1 + 2 + 3 + 6)/6 = 2
- 中央値 (median)
- データを一列にならべたときのちょうど真ん中の値: (1 + 2) / 2 = 1.5
- 最頻値 (mode)
- 最も頻繁に表れた値: 0
- 分散
- 各データの平均値からのずれの 2 乗和をデータ数で割ったもの:
(0 - 2) 2 + (0 - 2) 2 + (1 - 2) 2 (2 - 2) 2 + (3 - 2) 2 + (6 - 2) 2
= 4 + 4 + 1 + 0 + 1 + 4 = 14,

- 標準偏差
- データの平均値からの各標本のばらつき具合, 標準偏差は分散の平方根:

統計データの取りかた練習
統計のデータをとる仮想の練習をしてみよう。
標準偏差をとるには
標準偏差は、科学データであるならば、
実験がどれだけ精密に計測できたか(実験器具の不備や予想した論拠に間違いがないか)
を知る一つの目安となる。
例: やかまし村で計測された子どもたちの足の大きさ
| 名前 | 大きさ (cm) | 家 |
| リサ | 17.0 | 中屋敷 |
| ラッセ | 22.0 | 中屋敷 |
| ボッセ | 21.0 | 中屋敷 |
| オッレ | 23.0 | 南屋敷 |
| ブリッタ | 17.0 | 北屋敷 |
| アンナ | 16.0 | 北屋敷 |
| ピッピ | 25.0 | (ごたごた荘) |
| 平均 | |
| 最頻値 | 17.0 |
| 中央値 | 21.0 |
このデータにおいて、量的データは足の大きさであり、質的データは屋敷名である。
余談;日本では足の大きさは cm だが、北米、英国、
英国以外のヨーロッパでは、それぞれ異なるサイズ表示である。今回の例では、
日本式に従った。
演習:実際に電卓 (コマンドは xcalc &) を使って、
手計算で標準偏差まで求めよ。手順は以下の通り。
ワークシート
- 平均を求める
- 偏差を求める
- 偏差平方和を求める
- 分散を求める
- 標準偏差を求める
ワークシートはこのようになる。
| 名前 |
データ |
予想平均値( )
からの差 |
各データ-平均値 |
偏差=(各データ-平均値)2 |
| リサ |
17.0 |
|
|
|
| ラッセ |
22.0 |
|
|
|
| ボッセ |
21.0 |
|
|
|
| オッレ |
23.0 |
|
|
|
| ブリッタ |
17.0 |
|
|
|
| アンナ |
16.0 |
|
|
|
| ピッピ |
25.0 |
|
|
|
| 各「予想平均値からの差」の値の和 |
|
|
| 各「予想平均値からの差」の値の和/個数 |
|
| 平均値=予想平均値+各「予想平均値からの差」の値の和/個数 |
|
| 偏差平方和=各データの偏差の和 |
|
| 分散=偏差平方和/(個数-1) |
|
| 標準偏差=√分散 |
|
手計算のときにはとくに、有効数字について考える必要がある。
基本は、扱っている文字の桁数である。
よって小数第 2 位を四捨五入して求める。
相対度数
相対度数は、全体の度数で階級の度数を表したものになる。
統計の度数は、ここでは 7 人。階級を 16 ≤ x < 18,
18 ≤ x < 20, 20 ≤ x < 22, 22 ≤ x < 24,
24 ≤ x < 26, で考えると、
| 階級 | 度数 | 相対度数 |
| 16 ≤ x < 18 | 3 | 3/7 |
| 18 ≤ x < 20 | 0 | 0 |
| 20 ≤ x < 22 | 1 | 1/7 |
| 22 ≤ x < 24 | 2 | 2/7 |
| 24 ≤ x < 26 | 1 | 1/7 |
| 合計度数 | 7 | 相対度数 = 1 |
表計算の関数の使いかた
表計算の関数を知っている場合は、数式バーに直接書き込んで求める。
関数を知らない場合は、アクティブセルと数式バーの間の関数機能を駆使する。
Function Wizard を用いて、平均、モード、メジアンを求めることができる。
表計算ソフトを使って計算してみる
手計算ではかなり繁雑だった上記の情報を、
表計算ソフトで計算させることができる。Open Office を起動し、
Calc を使って今のデータを得よう。
%ooo3 &
で起動。データを入力する。
| 平均 | =AVERAGE(開始セル:終了セル) |
| モード | =MODE(開始セル:終了セル) |
| メジアン | =MEDIAN(開始セル:終了セル) |
| 標準偏差 | =STDEV(開始セル:終了セル) |
結果に注意せよ。
小数点を入力しても整数化され、また平均や標準偏差は、小数第 2 位まで求まってしまうが、
この数字の羅列はデータとして無意味である。
大規模なデータを整理するときに、
そもそもソフトウェアを用いたほうがいいのかどうか考えよ。
やかまし村 (人口 20 人)ではなく、首都ストックホルム (人口 80 万人)
で計測した場合、データ処理で喰われるメモリを想像すると ...!!
期待値とは、賭け事で平均どのくらい儲けることができるか、ということである。
確率変数
確率変数 X と 確率を P として、確率分布を書くことがある。
確率変数は、取りうる値のこと。
サイコロの確率変数は 1, 2, 3, 4, 5, 6 である。
事象について、起こりうる値が x1,
x2,
x3,
...
xn のとき、xk を取る確率を P(X=xk)
を pk と書くことにする。
これを一覧表にしたものを確率分布と呼ぶ。
コイントスとサイコロの確率分布を求めよ。
和の記号
全ての確率変数の取りうる確率は必ず 1 となる。
4 つの確率があるとき、
p1
p2
p3
p4 = 1
である。
確率変数がたくさんあるときは、これでは日が暮れてしまうので、
和の記号を使う。上の場合は
∑i=14pi = 1
一般に k 個ある場合
∑i=1kpi = 1
i は内部変数であり、よく j, k, m, n ... などが使われる。
度数分布
必要な語句をまとめる。
- 変量
- 調査されるものが数量で表されるもの
- 階級
- 資料を作成するために区分したそれぞれの区間
- 階級の幅
- 階級を表す区間の幅
- 階級値
- 階級の中央の値
- 度数
- それぞれの階級にある資料の個数
- 度数分布表
- 資料を整理して階級ごとの度数を示した表
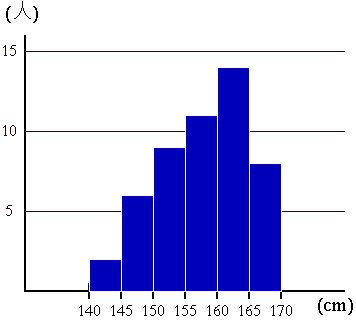
身長(cm)
以上 未満 |
人数(人) |
|---|
| 140〜145 | 2 |
| 145〜150 | 6 |
| 150〜155 | 9 |
| 155〜160 | 11 |
| 160〜165 | 14 |
| 165〜170 | 8 |
| 計 | 50 |
|---|
上の度数分布表について、次の問に答えよ。
- 階級の幅は何 cm か。
- 150 cm 以上 160 cm 未満の階級の度数を求めよ。
- 身長が 162.3 cm の人はどの階級に含まれるか。
- 各階級の幅は 5cm
- 2 つの階級の幅に属しているから、9 + 11 = 20
- 160 cm 以上 165 cm 未満
ヒストグラム
階級の幅を底辺、度数を高さとする柱状のグラフのこと。
それぞれの長方形の面積が階級の度数に比例する。
隙間をあけずに書く。(積分と関係する。)
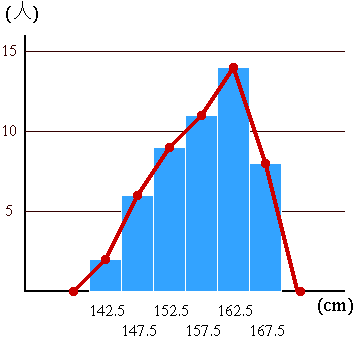
度数折れ線
ヒストグラムの各長方形の上辺の中点を順に結んで描いた折れ線グラフのこと。
両端は、階級値に対する度数を 0 とするのが規則。
あるクラス 20 人の走り幅跳びの記録は、
次の通りであった。
| 323(cm) | 261(cm) | 420(cm) | 375(cm) | 315(cm) |
| 408(cm) | 452(cm) | 441(cm) | 384(cm) | 501(cm) |
| 418(cm) | 463(cm) | 497(cm) | 514(cm) | 431(cm) |
| 422(cm) | 446(cm) | 436(cm) | 358(cm) | 399(cm) |
- 度数分布表を作成せよ。
- ヒストグラムを作成し、度数折れ線を書け。
記録(cm)
以上 未満 |
人数(人) |
|---|
| 200〜250 | |
| 250〜300 | |
| 300〜350 | |
| 350〜400 | |
| 400〜450 | |
| 450〜500 | |
| 500〜550 | |
| 計 | 50 |
|---|
相対度数
各階級の度数の全体に対する割合を相対度数という。
ある階級の相対度数 = その階級の度数 / 度数の合計
相対度数分布表: 階級とその相対度数を示した表。相対度数の合計は必ず 1 となる。
身長(cm)
以上 未満 |
人数(人) |
相対度数 |
|---|
| 140〜145 | 2 | 0.04 |
| 145〜150 | 6 | 0.12 |
| 150〜155 | 9 | 0.18 |
| 155〜160 | 11 | 0.22 |
| 160〜165 | 14 | 0.28 |
| 165〜170 | 8 | 0.16 |
| 計 | 50 | 1.00 |
|---|
下の表はある中学校の 1 年男子 25 人のソフトボール投げの記録
のようすを表したものである。次の問に答えよ。
-
空欄を埋めよ。
-
記録が 40 m 以上の生徒は全体の何 % か。
記録(m)
以上 未満 |
人数(人) |
相対度数 |
|---|
| 10 ∼ 20 | 2 | 0.08 |
| 20 ∼ 30 | 6 | |
| 30 ∼ 40 | 9 | |
| 40 ∼ 50 | 5 | |
| 50 ∼ 60 | 2 | |
| 60 ∼ 70 | 1 | |
| 計 | 25 | 1.00 |
|---|
-
(省略)
-
記録が 40 m 以上の生徒数は 5 + 2 + 1 = 8 (人)
したがって相対度数は 8 / 25 = 0.32
ゆえに 100 分率に直すと 0.32 × 100 = 32 %
下の度数分布表は、あるクラスの生徒が日曜日に新聞を
読んだ時間を表したものである。これについて、次の問に答えよ。
-
新聞を読んだ時間が 40 分未満である生徒は、全体の何 % にあたるか。
小数第 1 位を四捨五入して求めよ。
-
10 分以上 20 分未満の階級の相対度数が 0.15 であるとき、表中の x, y
の値を求めよ。
階級(分)
以上 未満 |
人数(人) |
|---|
| 0 ∼ 10 | 5 |
| 10 ∼ 20 | x |
| 20 ∼ 30 | 15 |
| 30 ∼ 40 | y |
| 40 ∼ 50 | 4 |
| 50 ∼ 60 | 2 |
| 計 | 25 |
|---|
- 40 分以上を読んだ生徒の人数は 4 + 2 = 6 (人) であるから、
40 分未満の生徒数は 40 - 6 = 34 (人) となる。
34 / 40 × 100 = 85 (%)
- 10 分以上 20 分未満の階級の相対度数が 0.15 なので、度数は
度数は x = 40 × 0.15 = 6 (人)
したがって
y = 40 - (5+6+15+4+2) = 8 (人)
代表値
代表値: 資料の分布のようすや全体的な傾向を表す値。
平均値(mean)、中央値(median)、最頻値 (mode) などがある。
- 平均値
- 変数をすべて足し合わせて資料の個数で割った値
- 仮平均
- 変量が大きくて計算が大変になる場合、
平均に近そうな適当な値を仮の平均を選ぶ。
その値からの差で平均を求め、
仮平均に加えて実際の平均を求める方法。
次の平均値を求めよ。
-
15, 20, 25, 30, 40
-
115, 120, 140, 125, 152
度数分布表から平均値を求めるには
度数分布表で、同じ階級に入っている資料は、
すべてその階級の階級値(中央の値)を持っていると考えて平均値を求める。
あるクラスで、ある日の家庭学習時間を調べたら、
下の度数分布表のようになった。このとき、次の問に答えよ。
-
表の「階級値」を埋めよ。
-
表の「階級値 × 度数」の欄を埋めよ。
-
家庭学習の平均時間を求めよ。
家庭学習(分)
以上 未満 |
階級値 |
度数
(人) |
階級値 × 度数 |
|---|
| 75 ∼ 85 | | 3 | |
| 85 ∼ 95 | | 6 | |
| 95 ∼ 105 | | 12 | |
| 105 ∼ 115 | | 11 | |
| 115 ∼ 125 | | 8 | |
| 計 | - | 50 | |
|---|
- 階級の中央値をとり、それぞれ 80, 90, 100, 110, 120
- それぞれ 240, 540, 1200, 1210, 960
- 学習時間の平均時間は 103.75
下の表はあるクラスの男子生徒全員がそれぞれ 1
回だけ垂直飛びを行い、その記録の結果をまとめた表である。
ただし x は (階級値) - (仮平均) の値を表している。
このとき、次の問に答えよ。
階級(分)
以上 未満 |
階級値
(cm) |
x
(cm) |
度数
(人) |
x × 度数 |
|---|
| 35 ∼ 40 | 37.5 | -10 | 2 | |
| 40 ∼ 45 | 42.5 | -5 | 4 | |
45 ∼ 50 | 47.5 | 0 | | |
| 50 ∼ 55 | | 5 | 4 | |
55 ∼ 60 | 57.5 | 10 | 3 | |
| 計 | - | - | 20 | |
|---|
-
表の空欄を埋めよ。
-
仮平均は何 cm か答えよ。
-
x × 度数の欄を全て埋めよ。
-
男子全員の記録の平均値を求めよ。
-
- 階級値の空欄は、50 ∼ 55 の階級の階級値であるので、52.5
- 度数の空欄は、20 - ( 2 + 4 + 4 + 3 ) = 7
-
表より、階級値 47.5 と仮平均の差が 0 であるので、仮平均は 47.5 cm
-
上から順に、-20, -20, 0, 20, 30
-
度数の総和は 10 なので、男子全員の平均値は 48 cm
最頻値は度数が最大である 7 人の 8 点。
中央値は、合計人数が 30 人で偶数なので、15 番目と 16 番目の値を求める。
15, 16 番目とも度数が 7 に含まれるので、7 点。
標本調査
アンケートでは、全ての数を調査するのではなく、
一部をうまく選ぶ。
選んだものが母集団の結果を反映しているかどうか吟味することを、
検定という。
- 母集団
- 調べようとするもとの集団全体の資料のこと
- 標本
- 調査のために選び出した資料のこと。
選び出すさいには無作為に選ぶ必要がある。
- 全数調査
- 調べようとする母集団の全ての資料をもれなく調べる方法
- 標本調査
- 標本を調査することにより、もとの母集団の性質や傾向を推定する方法
適切な調査方法
以下の調査について、適切な調査がどちらになるか、考えよ。
-
あるテストのクラスの平均点
-
テレビ局が行う世論調査
-
輸入食品の品質調査
-
学校で行う健康診断
-
テレビ番組の視聴率
-
蛍光灯の耐久時間の検査
-
全数調査: 人数は多くない。時間をかけずに正確な点数を求めることができる。
-
標本調査: 全体の傾向を知るために実施される。経費が節約できる。
-
標本調査: 全て検査すると商品が残らない。
-
全数調査: 個人の情報を全て収集する必要があるため。
-
標本調査: 全体の傾向を知るために実施される。経費が節約できる。
-
標本調査: 全て検査すると商品が残らない。
母集団比率と平均値の推定
- 標本平均
- 標本の平均値
- 推定
- 母集団から一定数の標本を多数回くり返して取りだし、各回の標本の比率や
平均値を求めることにより、母集団の比率や平均値にほぼ等しくなる。
標本から母集団の性質を見つけ出すこと。
ある政策についての世論調査で 400 人の標本の中で 250
人がその政策に賛成した。全体の何 % くらいが賛成していると考えられる
か。
250 / 400 × 100 = 62.5 ∼ 63
したがって 63 % くらい。
袋の中に白い球が入っている。その白球の個数を知るた
めに、触っただけでは白球と区別がつかない赤球 50 個をその袋の中に入れ、
よくかきまぜ、この袋の中から無作為に 30 個取りだして、白球と赤球の個数
を数えてもとに戻す実験をくり返したところ、下の図のようになった。このと
き、次の問に答えよ。
| 1 | 2 | 3 | 4 | 5 | 6 |
| 白球 | 24 | 23 | 26 | 24 | 25 | 25 |
| 赤球 | 6 | 7 | 4 | 6 | 5 | 5 |
-
この実験で 1 回に取りだされる白球の平均個数を求めよ。
-
袋の中には何個の白球が入っていると推定できるか。
-
24.5 個
-
1 回に取りだされる赤球の平均個数は、5.5 個。
白球と赤球の比は 24.5 : 5.5 なので、
袋に入っていた白球の数を x とすると
24.5 : 5.5 = x : 50
x = 222.72 ...
したがって 約 223 個。
指数の肩が複雑なとき



