数直線と数

自然数と整数

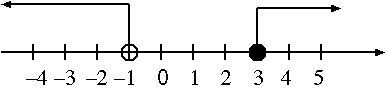
自然数とは、存在し、数えられる個数のことで、 1 から始まる。 整数とは、 0 や負の数を含み、 -∞ から ∞ までの小数値でない数である。 整数は i, j, k, l, m, n, ... を当てて任意の数を書くことが多い。

以上と以下、未満とより大きい

数直線上で、表すと分かりやすい。

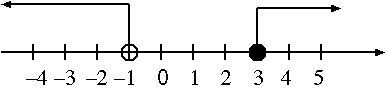
黒い丸はその数を含み、白い丸はその数を含まない。

ある数 x が 3 以上の整数である場合、 数式では x ≤ 3 と書き、4, 5, 6 .... が該当する。

ある数 x が 4 以下の整数である場合、 数式では x ≥ 4 と書き、4, 3, 2, 1 .... が該当する。

ある数 x が 5 より大きい整数の場合、 数式では x > 5 と書き、6, 7, 8, 9 .... が該当する。

ある数 x が 5 未満の整数の場合、 数式では x < 6 と書き、5, 4, 3, 2, 1 .... が該当する。

べき power

同じ数を何度かかけるとき、その個数を「乗」という。

場合の数

「場合の数を数える」　もれなく数え上げること

• 樹形図を書く
• 総当りの表を書く

という方法が素朴な方法。

積の法則

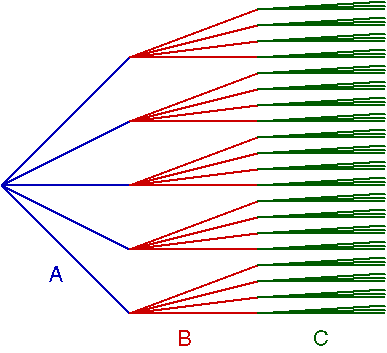
2 つの事象A, B があり、それぞれ起こる数は m, n 通りとする。 この場合 A, B がともに起こる場合の数は m × n 通りである。

樹形図

例を考えよう

樹形図の例

アイスクリームが 5 種類ある。そのうち 3 種類を選ぶ選び方は何通りあるか。

1. 1 種類目を5種類から選ぶ方法
2. 2 種類目を4種類から選ぶ方法
3. 3 種類目を3種類から選ぶ方法

和の法則

2 つの事象 A, B があり、同時には起こらないとする。 A, B が起こる数はそれぞれ m, n 通りとする。 この場合 A　またはB の起こる場合の数は m + n 通りである。

和の法則の例

大小2 つのサイコロの和が 5 または 10 になる場合の数は何通りか。

1. 和が 5
2. 和が 10

目の和の数が 5 または 10 になるのは、 大小のサイコロの目を (1, 2) のように書くとすると、 目の和の数が 5 となるのは

(1, 4), (2, 3), (3, 2), (4, 1)

(4, 6), (5, 5), (6, 4)

の 3 通り。

総当たりの表

総当たりの表から求めてみよう。

図から 7 通りと分かる。

階乗 factorial

ある整数 n から 1 までの数を順にかけ算した結果のこと。

整数 n (n = 0,1,2,...) の階乗: n × (n-1) × ... × 2 × 1 = n!

ただし、1! = 0! = 1 と定義しておく。

「ひとりひとつ」の条件で 3 兄弟にアイスクリームを出した。 バニラ、チョコレート、ストロベリーの 3 種類。 誰がどのアイスクリームを食べるか考えると何通りあるか？

「m 個全ての事象が重複を許さずに必ず 1 回ずつ起こる場合」、 これを数えると、階乗 (factorial) で表される。