分割統治法と再帰処理

分割統治法とは

複雑な問題を解決しようとするときは小さな問題に分けて取り組むと楽になる。例えば大きな数の掛け算をしたいときは、いっきに結果を求めることは難しいが以下のように筆算を使えば一桁づつ計算してわりと簡単に求められる。

         2 7 8
       x 4 6 3
      ―――――――――――
         8²3²4
     1 6⁴6⁴8
 + 1 1³1³2
―――――――――――――――――――
   1 2 8¹7¹1 4

このように、そのままでは解決しにくい大きな問題を複数の小さな問題に分割し、その全ての解を組み合わせることで元の問題を解決するアプローチは「分割統治法」と言い、プログラミングで頻繁に使われる。また、この問題解決手法を実施する方法として、「再帰」を用いることが多い。

再帰とは

あるものや手続きの中に、それ自身が現れることを再帰（recursion）という。プログラミングでは、ある手続き（Rubyではメソッド）の定義でその手続き自身を呼び出すことを再帰呼び出しといい、そのように定義することを再帰的定義という。

例えば、読んでいる本に知らない言葉（例：「膠着語」）がでてきたので国語辞典や百科事典でその意味を調べるという作業を考えよう。知識を持たない分野の専門用語であれば、その辞書定義にさらに分からない用語（例：「文法範疇」）が現れてそれらの意味まで調べないと説明を理解できない場合がある。こうして元の単語の意味を調べる手順の中で他の単語の意味を調べるというのは再帰の例である。

再帰を利用したプログラミング

プログラミングにしやすい例題を考えてみよう。自然数に対する階乗の(再帰的でない)定義は以下のようになる。

n の階乗（n!）とは
1から n までのすべての自然数を掛けたもの

例：

3! = 1・2・3 = 6

これを再帰的定義に直すと以下のようになる。

n の階乗とは
n-1 の階乗と n を掛けたものである。
ただし、1の階乗は1である。

例：

3! = 2!・3

それぞれの定義をRubyのメソッドにすると以下のようになる。

fact1.rb

# nの階乗を求めるメソッド(定義1)

def factorial(n)
  ans = 1
  i = 1
  while i <= n
    ans *= i
    i += 1
  end
  return ans
end

fact2.rb

# nの階乗を求めるメソッド(定義2)

def factorial(n)		# nのfactorial(階乗)とは
  if n == 1			# nが1なら
    return 1			# 答は1
  else				# そうでなければ
    return n * factorial(n-1)	# n と factorial(n-1)を掛けたもの
  end
end

定義1によるメソッドの動きに関しては、これまで学習したので説明を省略し、定義2によるメソッドについて考える。定義2のプログラム中赤色にした部分が再帰呼び出しとなっている。

たとえば、定義2のときに、factorial(5) と呼び出した場合を考えよう。

def factorial(n)		# ←n=5
  if n == 1			# 5 > 1 なので
    return 1			# ここには来ない
  else				# こっち↓
    return n * factorial(n-1)	# 5 と factorial(5-1)を掛けたもの
  end
end

n=5なので、1よりも大きくelse節内が評価される。すると、5 * factorial(5-1) を計算することになる。この時点では factorial(5-1) の値はまだ分からない。factorial(4) が呼ばれる。

def factorial(n)		# ←n=4
  if n == 1			# 4 > 1 なので
    return 1			# ここには来ない
  else				# こっち↓
    return n * factorial(n-1)	# 4 と factorial(4-1)を掛けたもの
  end
end

n=4なので、1よりも大きくelse節内が評価される。すると、4 * factorial(4-1) を計算することになる。ここでまた、factorial(3) が呼ばれる……。ということを繰り返すうちに、nがひとつずつ減っていき、最終的に factorial(1) が呼ばれ、factorial メソッドは1を返す。

実際に利用できるプログラムに直して実行してみよう。

　練習問題　 factorial.rb

#!/usr/koeki/bin/ruby
# -*- coding: utf-8 -*-

def factorial(n)
  if n == 1
    return 1
  else
    return n * factorial(n-1)
  end
end

puts "階乗を計算したい数を指定して下さい"
n = gets.to_i
printf("%dの階乗は%dです\n", n, factorial(n))

終了条件

上記の階乗の再帰的定義では、「ただし、1の階乗は1である」（if n == 1 return 1）という部分が重要である。再帰呼び出しでは同じメソッドを引数を変えて呼び出すことになるが、どこかで再帰呼び出しを止めないと延々と呼び出し続けることになってしまうので終わらない（システム上はメモリの限界が来てエラーで終わる）。この再帰呼び出しを止めるための条件を終了条件という。

再帰的メソッドのポイント

メソッドを再帰的に定義する場合、以下の点に注意する。

問題を分割して考えたときに、分割した部分を解く考え方と全体を解く考え方が同じである場合、再帰を使うことができる
問題分割を繰り返し、これ以上問題が分割できない場合に結果そのものを返す条件ブロックを入れる(終了条件)
分割した問題を再帰的に同じメソッドを呼んで得られた結果を合成したものを最後の結果として返す

階乗計算は再帰を用いず、ループを利用しても十分に簡単であるので、本来はループ処理で定義するのが自然である。しかし、複雑な問題になるとループと比べて再帰処理の方が使いやすくてソースコードが簡潔になる場合が多い。次節ではそのような例を見ていく。

クイックソート

前回はsortまたはsort_byメソッドを用いて配列の並べ替えをしたが、今回は再帰処理を応用したアルゴリズムの例である「クイックソート」を実装したプログラムを作成し、ソートに使ってみる。

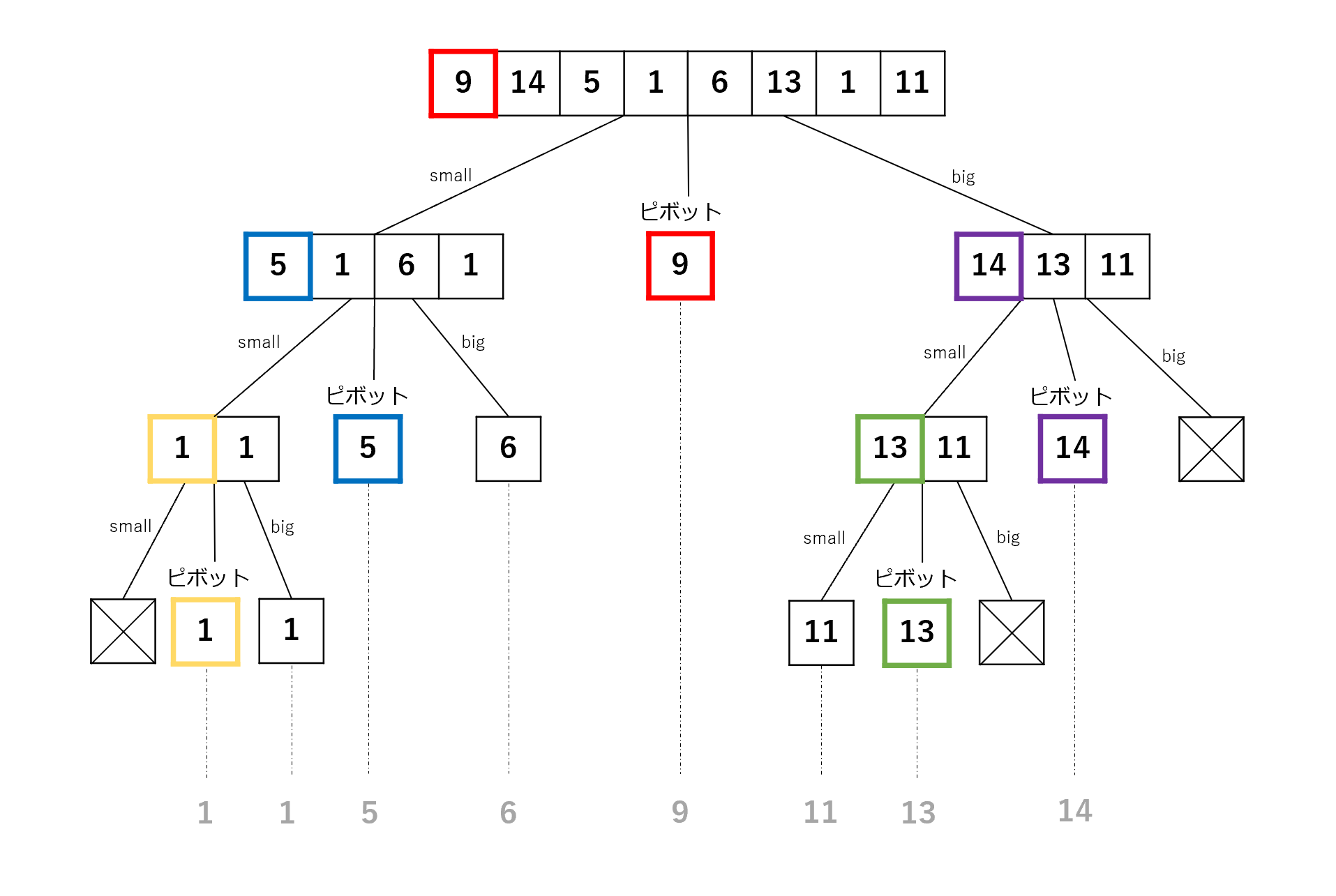
配列 x を対象に小さい順（昇順）でクイックソートを行う手順は下記の通りである。

配列 x の要素数が1個以下なら配列 x を返す（終了条件）。
配列 x から任意の要素を1個選ぶ（いわゆる「ピボット」；ここでは x[0] とする）。
x[0] 以外の各要素を x[0] と比較し、x[0] より小さい要素の配列 small と x[0] 以上の要素の配列 big に分ける。
配列 small に対してクイックソートを行い（再帰呼び出し）、配列 big に対してもクイックソートを行う（再帰呼び出し）。
配列 small をクイックソートした結果として返される配列、x[0]、配列 big をクイックソートした結果として返される配列の順に連結した配列を返す。

クイックソートのイメージ

次のプログラムはこのアルゴリズムを qsort というメソッドとして実装したものである。

　練習問題　 quicksort.rb

#!/usr/koeki/bin/ruby
# -*- coding: utf-8 -*-

def qsort(x)
    if x.length <= 1
      return x
    else
      small = []
      big = []
      for element in x[1..] # 配列 x[1] から比較する
        if element < x[0]
            small.push(element)
        else
            big.push(element)
        end
      end
      return qsort(small) + [x[0]] + qsort(big) # 再帰呼び出しと結果の合成。[x[0]] は x[0] の配列化
    end
end

# 適当な配列で動作確認しよう
original = [9, 0, 46, 70, 7, 24, 53, 40, 69, 33, 13]
print "　元の配列： "
p original
sorted = qsort(original)
print "ソートの後： "
p sorted

実行結果：

{c11xxxx}% ruby quicksort.rb
　元の配列： [9, 0, 46, 70, 7, 24, 53, 40, 69, 33, 13]
ソートの後： [0, 7, 9, 13, 24, 33, 40, 46, 53, 69, 70]

本日の課題

本日は提出する課題はない。

　基本課題　

「基礎プログラミングI」の第8回では下記のように10進数を2進数に変換する方法を習った。

元の10進数を2で割り商を下に、余りを右に書く
商をさらに2で割り商を下に、余りを右に書く
商が0になるまで繰り返す
最後に余りを下からの順に読む

例（250を2進数に変換）：
          [商] [余り]
250 / 2 = 125  → 0
125 / 2 =  62  → 1
 62 / 2 =  31  → 0
 31 / 2 =  15  → 1
 15 / 2 =   7  → 1
  7 / 2 =   3  → 1
  3 / 2 =   1  → 1
  1 / 2 =   0  → 1  ↑ 結果は下から上に読む
余りを下から上に読むと、10進数の 250 は2進数で 11111010 であるということが分かる。

この手続きを用いて与えられた10進数の整数を2進数に変換した結果を文字列として返すメソッド to_binary を再帰的に定義し、ユーザーが入力した数を変換し表示するプログラム num_converter2.rb を作成せよ。この変換方法は負の数に適用できないので、ユーザーが負の数を入力した場合はメッセージを表示しプログラムが終了する仕組みにすること。

ヒント：

この場合の再帰定義は次のようにまとめることができる：10進数 n を2進数にの変換した結果とは、n/2 を2進数に変換した結果の末尾に n%2 をつけたものである。ただし、n/2=0 の場合は変換結果は n%2 だけとなる。
ここで2進数は "0" や "1" を連結した文字列として表現する（to_s を使って剰余を文字に変換すること；文字列の結合は配列と同じく「+」を使える）。

実行結果の例：

{c11xxxx}% ruby num_converter2.rb
2進数に変換したい10進数を入力してください（0以上の整数）：
250
250 を2進数に変換すると 11111010 です。

　発展課題　

to_binaryメソッドを、再帰を使わずに書き換えてみよ。
qsortメソッドを書き変えて、数値の大きい順（降順）に並べ換えるようにせよ。
他に再帰処理で解決できる問題（Fibonacci数、ハノイの塔、文字列同士の編集距離など）について調べて、Rubyで実装してみよ。