自然言語処理(人間の言葉をコンピューターで分析する技術)で頻繁に使われる道具の一つとして「編集距離」(edit distance)がある。編集距離とは2つの文字列がどのぐらい異なっているか評価するための計量である。最も広く使われる編集距離の定義はレーベンシュタインという学者が提案した「レーベンシュタイン距離」(Levenshtein distance)である(単に「編集距離」と言えばレーベンシュタイン距離を意味することが多い)。
2つの文字列の間のレーベンシュタイン距離を計算するには、一つの文字列をもう一つの文字列に変換するに必要な1文字の変更処理の最小回数を求める。実行できる編集の種類は次の3つだけである:
たとえば、
問題:
次に、上記で説明した編集距離の計算アルゴリズムをC言語の関数として実装してみよう。一つ違う点として、紹介するプログラム(の一部)は文字列の先頭からではなく、末尾から処理を開始する設計になっている(先頭からスタートするのであれば、文字列の末尾に到達したかどうか調べるために関数を呼び出す度に文字列の長さを与えなければならないことになるが、後ろから先頭へ処理していく場合は最後の文字の添え字が必ず0になるので、長さは省略して良い)。なお、ここで紹介するプログラムは日本語の文字をはじめASCII文字以外の文字を含む文字列に対しては正しい結果を出さないので英語の例を使う。
編集距離の計算のように、簡単な作業を何回も繰り返しその結果を組み合わせることによって元の複雑な問題を解決できる場合、再帰処理を利用することが多い。以下のプログラムでは、再帰的に定義された関数 eddist を使ってレーベンシュタイン距離を求める。
levehshtein.c
#include <stdio.h>
#include <string.h>
int lowest(int values[], int n) { /* 整数の配列の中から最小値を返す */
int lowest = values[0];
int i = 0;
for (i = 1; i < n; i++) {
if (values[i] < lowest) {
lowest = values[i];
}
}
return lowest;
}
int eddist(char *str1, char *str2, int pos1, int pos2) {
/* 編集距離(レーベンシュタイン距離)を計算する関数
str1, str2 は対象の文字列
pos1, pos2 は現在見ている文字の位置(添え字+1)*/
int opt[3];
if (pos1 == 0) { /* str1の終わりに到達した場合、str2の残りの文字数を返す */
return pos2;
} else if (pos2 == 0) { /* str2の終わりに到達した場合、str1の残りの文字数を返す */
return pos1;
} else if (str1[pos1-1] == str2[pos2-1]) { /* 両方の文字列が対象の位置に同じ文字を持つ場合、次の位置に移動する */
return eddist(str1, str2, pos1-1, pos2-1);
} else {
opt[0] = eddist(str1, str2, pos1-1, pos2); /* str1から1文字を削除することと同じ */
opt[1] = eddist(str1, str2, pos1, pos2-1); /* str1に1文字を挿入することと同じ */
opt[2] = eddist(str1, str2, pos1-1, pos2-1); /* str1の1文字を置き換えることと同じ */
return 1 + lowest(opt, 3);
}
}
int main() {
int dist;
char str1[] = "programming";
char str2[] = "promising";
dist = eddist(str1, str2, strlen(str1), strlen(str2));
printf("Edit distance: %d\n", dist);
}
上記のプログラムは、一単語より長い文字列を与えると処理時間が長くなりあまり実用的ではない。計算の流れを分析してみれば、重複している処理が多いことが分かる。例えば、「cat」と「cast」の距離を求めるなら、 eddist(str1, str2, 1, 2) とそれ以降の4件の再帰呼び出しは2回繰り返され無駄がある。
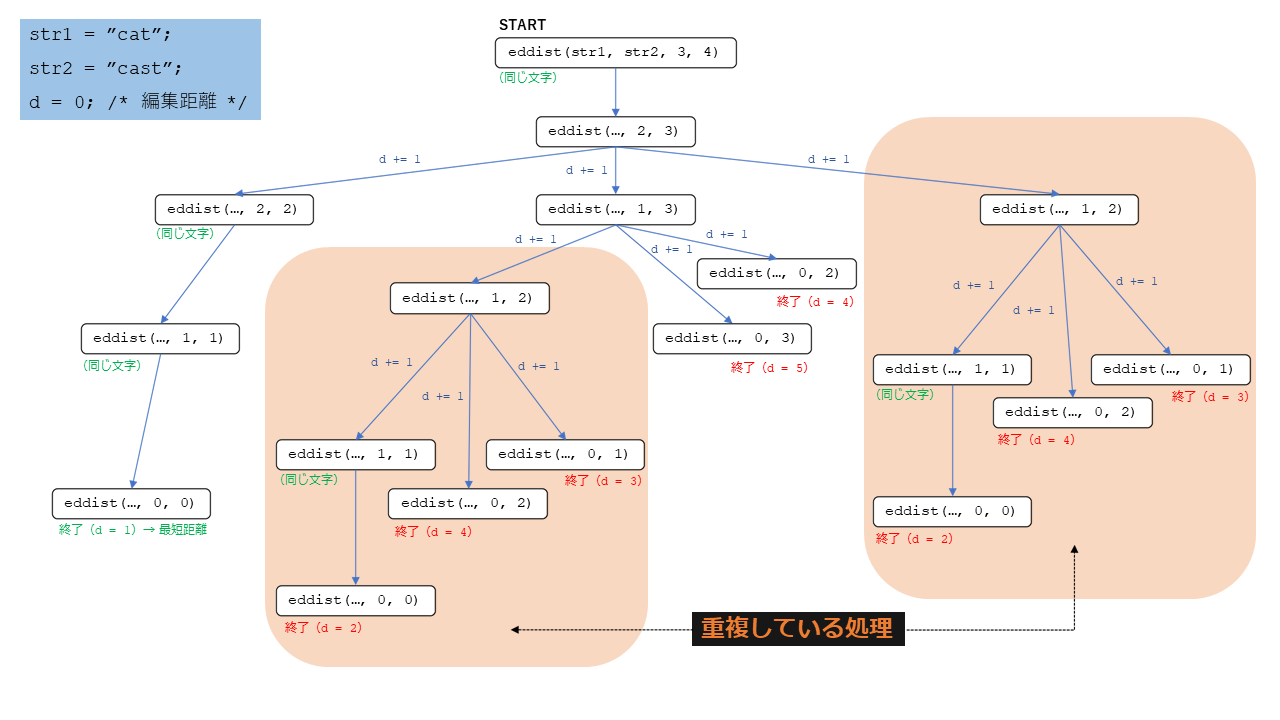
再帰呼び出しを行う度に処理が分岐する木構造になっているため、対象の文字列が長くなるに伴い必要な計算量が爆発的に増大してしまう。このような無駄を省くためには、一度計算した結果を保存(メモ化)し後で再び同じ処理を行う必要があれば記録された結果を再利用すれば良い。このような方法は「動的計画法」または「ダイナミック・プログラミング」(dynamic programming)と呼ばれる。次のプログラムでは、計算済みの編集距離を memo という(2次元)配列に保存することによって処理速度の大幅な加速化を実現している。
levehshteinDP.c
#include <stdio.h>
#include <string.h>
#define MAX_LEN 100 /* 対応できる文字列の長さの上限 */
int lowest(int values[], int n) { /* 整数の配列の中から最小値を返す */
int lowest = values[0];
int i = 0;
for (i = 1; i < n; i++) {
if (values[i] < lowest) {
lowest = values[i];
}
}
return lowest;
}
int eddist(char *str1, char *str2, int pos1, int pos2, int memo[MAX_LEN+1][MAX_LEN+1]) {
/* 編集距離(レーベンシュタイン距離)を計算する関数
str1, str2 は対象の文字列
pos1, pos2 は現在見ている文字の位置(添え字+1)
memo 既に計算した結果を保管するための表(2次元配列) */
int opt[3];
int dist;
if (memo[pos1][pos2] > 0) {
return memo[pos1][pos2];
} else if (pos1 == 0) { /* str1の終わりに到達した場合、str2の残りの文字数を返す */
return pos2;
} else if (pos2 == 0) { /* str2の終わりに到達した場合、str1の残りの文字数を返す */
return pos1;
} else if (str1[pos1-1] == str2[pos2-1]) { /* 両方の文字列が対象の位置に同じ文字を持つ場合、次の位置に移動する */
return eddist(str1, str2, pos1-1, pos2-1, memo);
} else {
opt[0] = eddist(str1, str2, pos1-1, pos2, memo); /* str1から1文字を削除することと同じ */
opt[1] = eddist(str1, str2, pos1, pos2-1, memo); /* str1に1文字を挿入することと同じ */
opt[2] = eddist(str1, str2, pos1-1, pos2-1, memo); /* str1の1文字を置き換えることと同じ */
dist = 1 + lowest(opt, 3);
memo[pos1][pos2] = dist;
return dist;
}
}
int main() {
int dist;
char str1[] = "programming is fun!";
char str2[] = "promising young man";
int memo[MAX_LEN+1][MAX_LEN+1] = {0}; /* 全ての要素を 0 に初期化 */
dist = eddist(str1, str2, strlen(str1), strlen(str2), memo);
printf("Edit distance: %d\n", dist);
}
プログラムの中で関数が呼び出されると、メモリのスタック領域で「スタックフレーム」と呼ばれるブロックが割り当てられ、そこで関数の処理に必要な情報(関数の中で使われる変数など)が格納される。たとえば、以下のプログラムを実行すればスタックメモリは図のように使用される。
#include <stdio.h>
int my_func2(int z) {
z += 2;
return z; /* my_func2 のスタックフレームが除外される */
}
int my_func1(int y) {
y++;
y = my_func2(y); /* 新しいスタックフレームが作成される */
return y; /* my_func1 のスタックフレームが除外される */
}
int main() {
int x = 0;
my_func1(x); /* 新しいスタックフレームが作成される */
return 0; /* main のスタックフレームが除外される */
}
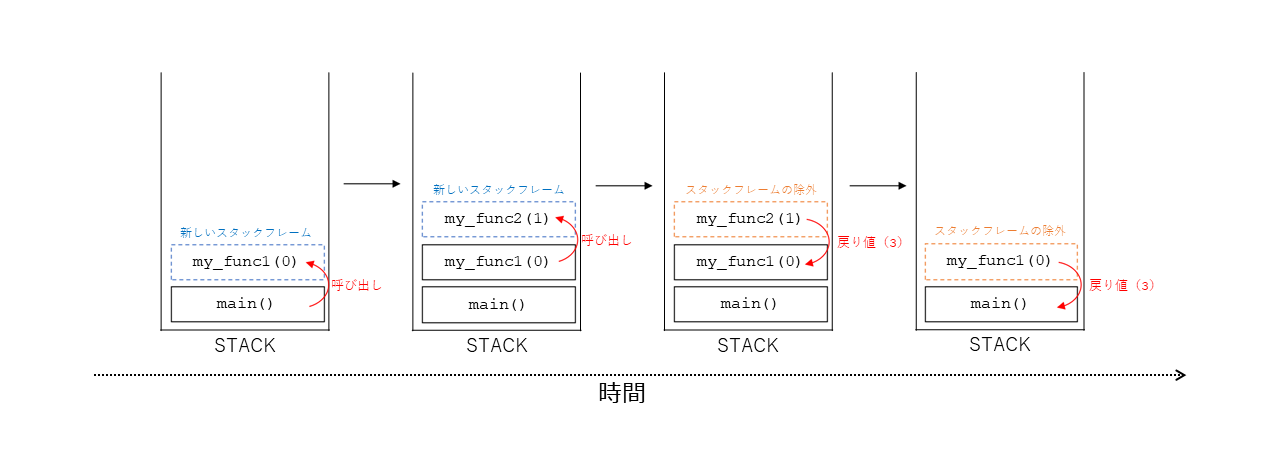
関数の実行が終了した後はそのスタックフレームが除外され解放されたメモリを再利用できる。しかし、再帰的に定義された関数の場合は関数から抜ける前に次の呼び出しが行われるので、再帰の終了条件が成立するまでスタックメモリの消費量が増えていく一方である。
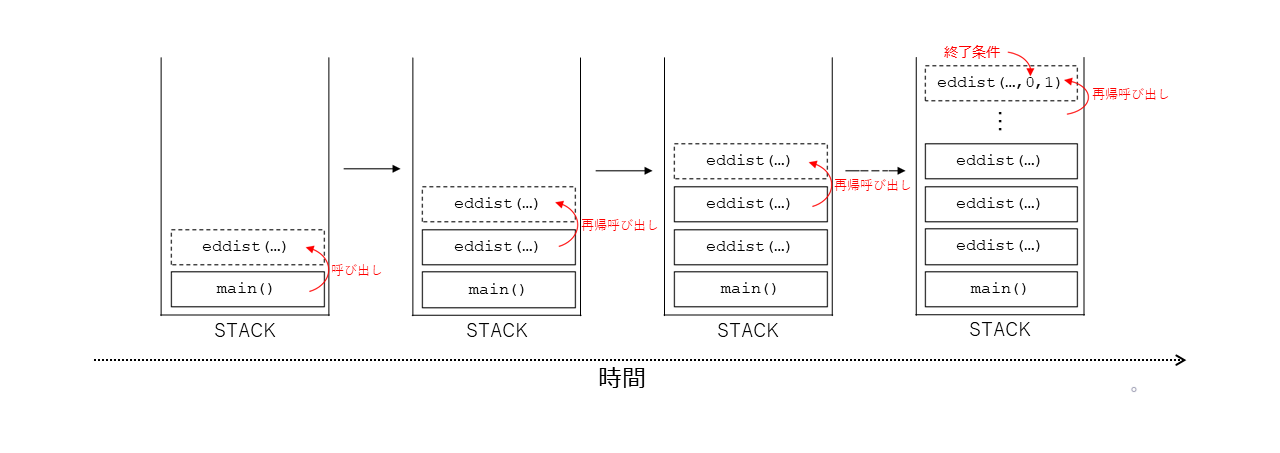
再帰が深くなるとスタックが溢れてしまい(スタックオーバーフロー)プログラムの実行が中断されるおそれがある。下記のプログラムを実行して確かめよう(数字を1ずつ増やしながら再帰呼び出しを行うことを無限に繰り返すプログラムである)。
stack_overflow.c
#include <stdio.h>
int infinite_rec(int x) { /* 無限に再帰呼び出しを行う関数 */
if (x%1000 == 0) {
printf("%d\n", x);
}
x++;
return infinite_rec(x);
}
int main() {
infinite_rec(0);
return 0;
}
当然、関数を呼び出す度に必要なメモリが多いほど、スタックオーバーフローが発生するのも早くなる。
stack_overflow_faster.c
#include <stdio.h>
int infinite_rec(int x) { /* 無限に再帰呼び出しを行う関数 */
char txt[] = "これでスタック要領のメモリがより早く消費されエラーを起こす";
if (x%1000 == 0) {
printf("%d\n", x);
}
x++;
return infinite_rec(x);
}
int main() {
infinite_rec(0);
return 0;
}
一方で、for文やwhile文などによる反復処理(ループ)の場合は、処理を繰り返す度に同じスタックフレームが再利用されるため、上記のような問題がない。上記の再帰的関数をループに書き換えればエラーが出なくなる。
iterative.c
#include <stdio.h>
int infinite_loop(int x) { /* 無限に繰り返し処理を行う関数 */
int i = 0;
while (i==0) {
char txt[] = "ループの場合はスタックが溢れるという問題が発生ない";
if (x%1000 == 0) {
printf("%d\n", x);
}
x++;
}
return x;
}
int main() {
infinite_loop(0);
return 0;
}
このような再帰処理の弱点を踏まえて、長い文字列にも対応できる編集距離の計算プログラムを作りたいならループを使って実装した方がいい(実際にこれまで紹介したプログラムは本学の端末で実行する場合、対応できる文字列の文字数は1400程度が上限であり、MAX_LEN をそれより高い値に設定すればエラーになる)。具体的には、ダイナミック・プログラミングを使ったプログラムの memo(計算結果を記録する表)を一つのループの中で作成する仕組みにすれば再帰呼び出しを行う必要がなくなる。
str1 = "SPARTA"
str2 = "SPORT"
以下のプログラムは再帰呼び出しを行わずにレーベンシュタイン距離を計算する。
levenshtein_loop.c
#include <stdio.h>
#include <string.h>
#define MAX_LEN 100 /* 対応できる文字列の長さの上限 */
int lowest(int values[], int n) { /* 整数の配列の中から最小値を返す */
int lowest = values[0];
int i = 0;
for (i = 1; i < n; i++) {
if (values[i] < lowest) {
lowest = values[i];
}
}
return lowest;
}
int eddist_iter(char *str1, char *str2, int len1, int len2) {
/* (再帰呼び出しを使わずに)編集距離(レーベンシュタイン距離)を計算する関数
str1, str2 は対象の文字列
len1, len2 は文字列の長さ */
int matrix[MAX_LEN+1][MAX_LEN+1];
int i, j;
int opt[3];
for (i = 0; i <= len1; i++) {
for (j = 0; j <= len2; j++) {
/* str1の終端に到達した場合、str2の残りの文字数を返す */
if (i == 0) {
matrix[i][j] = j;
/* str2の終端に到達した場合、str1の残りの文字数を返す */
} else if (j == 0) {
matrix[i][j] = i;
/* 両方の文字列が対象の位置に同じ文字を持つ場合、編集距離は増えない */
} else if (str1[i-1] == str2[j-1]) {
matrix[i][j] = matrix[i-1][j-1];
/* 対象の位置にある文字が異なる場合、可能な編集を全て検討し
最小値を求める */
} else {
opt[0] = matrix[i][j-1]; /* str1に1文字を挿入することと同じ */
opt[1] = matrix[i-1][j]; /* str1から1文字を削除することと同じ */
opt[2] = matrix[i-1][j-1]; /* str1の1文字を置き換えることと同じ */
matrix[i][j] = 1 + lowest(opt, 3);
}
}
}
/* 処理が終わったら表の最後のセルに最小距離が入っているのでそれを返す */
return matrix[len1][len2];
}
int main() {
int dist;
char str1[] = "programming is fun!";
char str2[] = "promising young man";
dist = eddist_iter(str1, str2, strlen(str1), strlen(str2));
printf("Edit distance: %d\n", dist);
}
再帰呼び出しをなくすことでスタックフレームの数を減らすことができたが、実はこのプログラムのメモリ消費の面でもっと深刻な問題があり、まだ長い文字列に対応できない。なぜなら、計算結果を記録する2次元配列(matrix)に必要なメモリ要領は MAX_LEN の二乗に比例している。たとえば、最大で1000文字までの文字列の編集距離を計算したいなら、1,000 * 1,000 = 1,000,000セルの表を格納できるメモリを確保しなければならない。
しかし、ソースコードを見たら編集距離の計算を実行する中で実際に参照されるのは現在の添え字(i, j)の要素か、その直前(i-1, j-1)の要素だけであることが分かる。この性質を利用すれば、2行だけの表で同じ処理を行うことができる。具体的には、内側のループで今回新たに求まる値を1行に、そしてもう1行には前回の結果を保管し外側のループで常に更新する。このように改良したプログラムのメモリ消費は MAX_LEN の二乗ではなく MAX_LEN に比例するため、以下の例のように一万文字の文字列にも対応できるようになる。
levenshtein_loop2.c
#include <stdio.h>
#include <string.h>
#define MAX_LEN 10000 /* 対応できる文字列の長さの上限 */
void swap_pointers(int **p2p1, int **p2p2) {
/* 2つのポインタが指すアドレスを交換する */
int *temp = *p2p1;
*p2p1 = *p2p2;
*p2p2 = temp;
}
int lowest(int values[], int n) { /* 整数の配列の中から最小値を返す */
int lowest = values[0];
int i = 0;
for (i = 1; i < n; i++) {
if (values[i] < lowest) {
lowest = values[i];
}
}
return lowest;
}
int eddist_iter(char *str1, char *str2, int len1, int len2) {
/* (再帰呼び出しを使わずに)編集距離(レーベンシュタイン距離)を計算する関数
str1, str2 は対象の文字列
len1, len2 は文字列の長さ */
int row1[MAX_LEN+1] = {0};
int row2[MAX_LEN+1] = {0};
int *prev = row1; /* 直前の行 */
int *current = row2; /* 今見ている行 */
int i, j;
int opt[3];
for (i = 0; i <= len1; i++) {
for (j = 0; j <= len2; j++) {
/* str1の終端に到達した場合、str2の残りの文字数を返す */
if (i == 0) {
current[j] = j;
/* str2の終端に到達した場合、str1の残りの文字数を返す */
} else if (j == 0) {
current[j] = i;
/* 両方の文字列が対象の位置に同じ文字を持つ場合、編集距離は増えない */
} else if (str1[i-1] == str2[j-1]) {
current[j] = prev[j-1];
/* 対象の位置にある文字が異なる場合、可能な編集を全て検討し
最小値を求める */
} else {
opt[0] = current[j-1]; /* str1に1文字を挿入することと同じ */
opt[1] = prev[j]; /* str1から1文字を削除することと同じ */
opt[2] = prev[j-1]; /* str1の1文字を置き換えることと同じ */
current[j] = 1 + lowest(opt, 3);
}
}
swap_pointers(&prev, ¤t); /* 今回調べた行(current)が今度 prev になる */
}
/* 処理が終わったら prev の最後の要素に最小距離が入っているのでそれを返す */
return prev[len2];
}
int main() {
int dist;
char str1[] = "CGTGCAACCCCTATCGCCATCGATTGTTTCTGCGGACGGTGTTGTCCTCATAGTTTGGGCATGTTTCCCTTGTAGGTGTGAAACCACTTAGCTTCGCGCCGTAGTCCTAAAGGAAAACCTATGGACTTTGTTTCGGGTAGCACCAGGAATCTGAACCATGTGAATGTGGACGTGGCGCGCGTACACCTTAATCTCCGGTTCATGCTAGGGATGTGGCTGCATGCTACGTTGACACACCTACACTGCTCGAAGTAAATATACGAAGCGCGCGGCCTGGCCGGAGCCGTTCCGCATCGTCACGTGTTCGTTTACTGTTAATTGGTGGCACATAAGCAATATCGTAGTCCGTCAAATTCAGCCCTGTTATCCCCGGCGTTATGTGTCAAATGGCGTAGAACTGGATTGACTGTTTGACGGTACCTGCTGATCGGTACGGTGACCGAGAATCTGTCGGGCTATGTCACTAATACTTTCCAAACGCCCCGTATCGATGCTGAACGAATCGATGCACGCTCCCGTCTTTGAAAACGCATAAACATACAAGTGGACAGATGATGGGTACGGGCCTCTAATACATCCAACACTCTACGCCCTCTTCAAGAGCTAGAAGGGCACCCTGCAGTTGGAAAGGGAATTATTTCGTAAGGCGAGCCCATACCGTCATTCATGCGGAAGAGTTAACACGATTGGAAGTAGGAATAGTTTCGAACCACGGTTACTAATCCTAATAACGGAACGCTGTCTGAAGGATGAGTGTCAGCGAGTGTAACTCGATGAGCTACCCAGTAGTCGAACTGGGCGAGACAACCCGGCGCTAATGCACTCAATCCCGAGGCCTGACGCGACATATCAGCTTAGACTAGGGCGGGGGTGTTGACGTTTGGGGTTGAATAAATCTATTGTACTAATCGGCTTCAACGTGCCCCACGGGTGGCACCTCAGGAGGGGCCCACAGCGAGGAAGTAAACTGTTATTCGTCGGCGATGGTGGTAGCTAATTATGTTCCTTGCCACTACAATAGTATCTAAGCCGTGTAATGGGAACATCCACACTTTAGTGAATCGATGCGCGGCTTCAGAATACCGTTTTGGCTACCTGTTACTAAGCCCATCGTGGTTTTCAGATATCGTGCACGTAGGGTTGCACCGCACGCATGTGGAATTAGTGGCGAAGTACGATTCCACGACCGACGTACGATTCAACTATGCGGACGTGACGAGCTTCTTTTATATGCTTCGCCCGCCGGACCGGCCTCGTGATGGGGTAGCTGCGCATAAGCTTATGACAATTAACGAGTGTGTACTCGTTTTATCATCTCACAGTTAAAGTCGGGAGAATAGGAGCCGCTACACACAATTTACCGCATCTAGACCTAACTGAGATACTGCCATAGACGACTACCCATCCCTCTGGGCCTTAGATAGCCGGATACAGTGACTTTGAAAGGTTTGTGGGGTACAGCTATGACTTGCTTAGCTGCGTGTGGGGGAAGGAACTTTTGCGTGTTAGTATGTTGACCCGTGTATTACGCATGCGGGTAGATTATGTAGGTAGAGACATCCAGGTCAAGTTCTCGACCTTCTCGTGGGAGGTGAACCAGTTCACTATAGGACCATTCCGTTCGAGCATGGCACTAAGTACGCCCTCCCCATTCTGGTAATCTTCATCCCTATCAGGGCTTGGAGTGAATGGTGAGGGTTATTCCCCAGGAACAGACTTCCTACTCACAGTCGGTCACATTGGGCTACTCCTTGGGTCTTCGGCTTGACCCGGTCTGTTGGGCCGCGATTGCGTGAGTTTCGGCCCTGCGCTGCGCTGTATAGCCGATTCTCATCCGGGCCTCACATCTGGAAACCCCAACCTATTTAGACAGCATCATTGGCCGAAGTTGCTGGGCATGTCCACCGTGAAGTCCTCCCCGGGCGTCCCTCCTTCAAAAGACGATAAGCTCCGGCAAGCACCATTGATCAACGCAAGGATCGGTGATGTTAACAAAGATTCGGCACATTACTCTTGTTGGTGTGGTATCGCTTAACTGCGCGGCGGAGCCTTATGGCAAAACCGTTCGGGAATGATTCCGGTAGCGCTAAAGGTCCATAGCACGTACATCGCAACCTGGCGTGCGTTCAATTTGACGACCGCTTGGCGCTAAGGTGCTGGCCACGTGCTAAATTAAAGCGGCTGCACTGCTGTAAGGACGATTACGGAGTGGGCGGCCTGGGGGGAGCACTACCCCATCGACCTGTACAGGAACACTCTATATTGCTCTCAGACGAACAAATTACTAGAGTGCCGCTTTCAGCCCCCCTGTCGTCGCCGACGTCTGTAATATGGCGTTGTTGTGATTCGACTCTATTGAGGCATCAACTGATGCGTAAGGAGATCTGGAATGAATTGGCCTATGTCACTGAAACTGTCCAAACACCCAATGTCGTTAGTGAAGGTTCTGACGCATACCTCCTTCGTTGAGAACTCACAATTATACAACTGGGGACATAATCCCTACGCCCATCATCTACACGCGTCTCTGTGGCTCCAGTTCATGTATTGGGAGAGTATCCTCCACAAGATCTAGTGGTATGGTGGTATAGTAAGCTCGTACTGTGATACACGCGACAGGGGTAGGACCATCAGTAATAGGGATAGTGCGAAAGCTCACTGACCACTGCCTATAGGGGGTGCTTACTTTTAGAAAAAGTGTCAGCCAGTATAACCCCACGAGGATTCGAAAAGGTGAACCGAGCCAGACAATCCGGAGGCACGGGGCTCAAAGCCGCGACACGACGGCTCTCGGCCGGTAACAGTAACCCCGGAGTGAACACCTATGGGGCTGGATAAAACTGCCCTGGTGAGCGCCATCAGCAACCCGAATACGTGGCATTTCAGGAGGCGGCCGGAGGGGGGATGTCTTCTACTATTCGAGGCCGTTCGTTAATACTTGTTGCGTTCCTAGCCGCTATATTTGTCTCTTTGCCGACTAATGTGAACAACCACACCATAGCGATTTATCGGAGCGCCTCGGAATACGGTATGAGCAGGCGCCTCGTGAGACCATTGCGAATACCAGGTATCGTGTAAGTAGCGAAGGCCCGTACGCGAGATAAACTGCTAGGAAACCGCGTCTCTACGACCGGTGCTCGATTTAATTTCGCTGACGTGATGACATTCCAGGCAGTGCGTCTGCTGCCGGGTCCCTCTCGTGATTGGGTAGTTGGACATGCCCTTGAAAGACATAGCAAGAGCCTGCCTCTCTATTGATGTCACGGCGAATGTCGGGGAGACAGCAGCGGCTGCAGACATTACATCGGAGTAACACTAAGGTGGGATAACTCCGTAACTGACTACGCCTTTCTCTAGACCTTACTTGACCAGATACACTGTCTTTGACACGTTGATGGATTAGAGCAATCACATCCAAGACTGGCTATGCACGAAGCAACTCTTGAGTGTTAAAATGTTGTCTCCTGTATTCGGGATGCGGGTACTAGATGACTGCAGGGACTCCGACGTTAAGTACATTACCCTGTCATAGGCGGCGTTCAGGATCACGTTACCGCCATATGATGCGAGCATGACATCATCTCCGCTGTGCCCACCCCAGTAGTGATTATTCCTATAACCCTTCTGAGTGTCCGGAGGCGGAAATCCGCCACGAATGAGAATGTATTTCCCCGACAATCATAATGGGGCGCTCCTAAGCTTTTCCACTTGGTTGGGCCGGCTAGGCCTCTCTGCCCGGAGTTTCGGCGCACTGCTGCCGACAGCCGGGCATTGTTTTAGGGGCGTTATTCGAGGGCACTCGGAGCTAACTTGTCGGGACCAGCCGGGGTAGTCATCGGGCTTATACAGCGAAAAGCCCAGGACCCGGCTCCACGCTATGGAACGTCTTTAGCTCCGGCAAGCAATTAAGAACAACGCAAGCATCGCGGATATAAACAGAGAAACGGCCGAATACACCTGTTCGTATCGTATCGGTAAATAGCCTCGCGGAGCCATGTGCCATACTGGTCTGCGGAGCACTCTGGTTATGCATATGGTCCACAGGACACTCGTCGCTTCCGGGTATGCGCTCTATGTGACGGTCTTTAGGCGCACTAATGCTCAGCACCATTTAAACCAGACCGACACCAGATCTGTAAGGTCCGCCACGCAGACGACAGCCCACGGAGATCACCGACCGATCTATCTGATCGGCGACCATTTGTGTGGTACTGGGGCGGAGAGGTAACTACGGTGCCGCTAACAACCCCTCTGTCGTCGCTGACGTTTGTAGTCTAGTCTCATTATGATTGTACGCTATTCAGGGATTGACTGATACCGGAAGACATCTCAGTTGAAGTGGTCTATACGACAGAGACCGTGCACCTACCAAATCTCCTTAGTGTAAGTTCAGACCAATTGGTAGTTTGTCCAGAACTCAGATTTTAACAGCAGAGGACGCATGCTCTACCTTCATGATCCACTGACGTCCCTGAGGCTGCAATACATGCAACGAGGCAGTCTCCGCGGTAAGTCCTAGTGCAATGGCGCTTTTTTACCCTCGTCCTCGAGAAGAGGGGACGCCAGTGCAGATATCTTTAATGTGGTAATTGGGAGGACTCTTGGCCCTCCGCCCTTAGGCAGTGCATACTCTTCCATAAACGGGCTGTTAGTTATGGCGTCCGAGGATTCAAAAAGGTGAGCGAACTCGGCCGATCCGGAGAGACGGGCTTCAAAGCTGCCTGACGACGGTTGCGCGTCCGTATCAAAATCCTCCTAATAAGCCCCCGTCACTGTTGGTTGAAGAGCCCAGGACGGGTTGGCCAGATGTGCGATTATATCGCTTAATGGCTCTTGGGCCGCGGTGCGTTACCTTGCAGGAATTGAGGCCGTCCGTTAATTTCCCTTGCATACATATTGCGTTTTTTTGTCTTTTTATCCGCTTACTTAGATAAGAGTGACATAGCTTCTTACCGGAGCGCCTCCGTACACAGTACGATCGCACGCCCCATGAGATCGATAGGTATACCAGGTGTCCTGTGAGCAACGAAAGCCTAAACGGGAAATACGCGGCCAAAAGTCGGTGCGAATACGAGTCGTAGCAATGTTGGTCTGGCTATGATCTACATATTTCAGGCGGTACGTCTGCTCTGGTCAGCCTCTAATGGCTCGTTAGATAGTCTAGCCGCTGGTAATCACTCGATGACCTCGGCTCCCCATTGGTGCTACGGCGATTCTTGGAGAGCCAGCTGCGATCGCTAATGTGAGGACAGTGTAATATTAGCAAGCGATAAGTCCCCAACTGGTTGTGGCCTTTTGAAAAGTGAACTTCATAACATATGCTGTCTCACGCACATGGATGGTTTGGACAAATTTGATTCAAGTCTGATCAACCTTCACACAGATCTAGAATCAAAAGCAGTGATCTCCCGGGTGCGAAATAAAAATACTAGGTAACTAGAGGGACTGCGACGTTCTAAACGTTGGTCCGTCTGAACCGCCATCCAGGATCACGTCGCCCCGAAAAAAAGATATCAGGAACTCTCCTCCTCAGCAGTCAGGTCTATGGAAACTACAGGACTAACCTTCCTGGCAACCGGGGGGTGGGAATCCGTCACATATGAGAAGGTATTTGCTCGATAATCAATACTCCAGGCATCTAACTTTTCCCACTGCCTTAAGCCGGCTTGCCCTTTCTGCCTGTAGATCCATAGGACTCGTGCCAACGCGCAGGCATAGTTCGAGGAGAAATATCCGGGGCCAAAGACAACCAGCATCTCGGGTCTTGCCCAACCCGCCTACATGCTGTTATAGCGAATCAGTGGAAACCCGGTGCCAGGCGATGGAATGTCCTTAACTCTGGCAGGAAATTAAAGGGAACGTATATACAACGCAAAGAAGCTGGAAAATTGGCGAGAGAATCTTCTTTCTGTCTATCGAAGAATGGGCATGGGGTGGCAACCGTCATGCTAGCGTGCGGGGTGCACTTGGTAACCATTTGGGACACCGGACACTCGCTGTTTTCGAAATTACCCTTTAAGCGCGGGTATTGAACCAGGCTTATGCCCAGCATCGTTGCAAGCAGACTCAAACTAGATATATTATGCCCGCCATACAGACGAAACTAGTCGGAGATTATCGAGCATACTATCACGTCGGCGACCACTAGTGAGTTACTAGAGCCGAGGGGCAACGTTGATGCCCCTAAGAACCTCTGGCTCGACGCAAGCCATAACACCCCTGTCACATCATAATCGTTTGCAATTCAGGGCTTGATCAACACTGGATTGCCTTTCTCTTAAAGTATTATGCAGGACGGGGTGCGCGTACCATGTAAACCTGTTATAACTTACCTGAGACTAGTTGGAAGTGTGGCTAGATCTTAGCTTACGTTTCTAGTCGGTCCACGTTTGGTTTTTAAGATCCAATGATCTTCAAAACGCTGCAAGATTCACAACCTGCTTTACTAAGCGCTGGGTCCTACTGCAGCGGGACTTTTTTTCTAAAGACGTTGAGAGGAGCAGTCGTCAGACCACATAGCTTTCATGTCCTGATCGGAAGGATCGTTGGCGCCCGACCCTTAGACTCTGTACTGAGTTCTATAAACGAGCCATTGCATACGAGATCGGTAGATTGATAAGGGACACAGAATATCCCCGGACGCAATAGACGGACAGCTTGGTATCCTAAGCACAGTCGCGCGTCCGAACCTAGCTCTACTTTAGAGGCCCCGGATTCTGGTGCTCGTAGACCGCAGAACCGATTGGGGGGATGTACAACAATATTTGTTAGTCACCTTTGGGTCACGATCTCCCACCTTACTGGAATTTAGTCCCTGCTATAATTTGCCTTGCATATAAGTTGCGTTACTTCAGCGTCCTAACCGCACCCTTAGCACGAAGACAGATTTGTTCATTCCCATACTCCGGCGTTGGCAGGGGGTTCGCATGTCCCACGTGAAACGTTGCTAAACCCTCAGGTTTCTGAGCGACAAAAGCTTTAAACGGGAGTTCGCGCTCATAACTTGGTCCGAATGCGGGTTCTTGCATCGTTCGACTGAGTTTGTTTCATGTAGAACGGGCGCAAAGTATACTTAGTTCAATCTTCAATACCTCGTATCATTGTACACCTGCCGGTCACCACCCAACGATGTGGGGACGGCGTTGCAACTTCGAGGACCTAATCTGACCGACCTAGATTCGGCACTGTGGGCAATATGAGGTATTGGCAGACACCCAGTGCCGAACAACACCTGACCTAACGGTAAGAGAGTCTCATAATGCGTCCGGCCGCGTGCCCAGGGTATATTTGGACAGTATCGAATGGACTGAGATGAACCTTTACACCGATCCGGAAACGGGTGCGTGGATTAGCCAGGAGCAAACGAAAAATCCTGGGCTACTTGATGTCTTGTGACGTTCTTAGAGATGGACGAAATGTTTCACGACCTAGGATAAGGTCGCCCTACAAAATAGATTTGTGCTACTCTCCTCATAAGCAGTCCGGTGTATCGAAAGAACAAGACTAGCCTTGCTAGCAACCGCGGGCTGGGGGGCTAAGGTATCACTCAAGAAGCAGGCTCGGTAACATACGGTCTAGCTATCTGACTATCGCCTACGTCATATAGGGACCTATGATATCTGCGTGTCCAACCTTAGAATTCACTTCAGCGCGCAGGTTTGGGTCGAGATAAAATCACCAGTACCCAAGACCACGGGCGCTCGGCGCCTTGGCTAATCCCGGTACATGTTGTTATAAATAATCAGTAGAAAATCTGTGTTAGAGGGTCGAGTCACCATATATCAAGAACGATATTAATCGGTGGGAGTATTCAACGTGATGAAGACGCTGGGTTTACGTGGGAATGGTGCTTCTGTCCTAACAGGCTAGGGTATAATGCTGAAACCGTCCCCCAAGCGTTCAGGGTGGGGTTTGCTACGACTTCCGAGTCCAAAGTGTCCGTGTTTTTGATATATACGCTCAAGGGCGAGAATTGGACCTGGCTTACGTCTTAGTACGTAGCATGGTGACACAAGCACAGTAGATCCTGCCCGCGTTTCCTATATATTAAGTTAAATCTTATGGAATATAATAACATGTGGATGGCCAGTGGTCGGTTGTTACACGCCTACCGCAATGCTGAAAGACCCGGACTAGAGTGGCGAGATCTATGGCGTGTGACCCGTTATGCTCCATTTCGGTCAGTGGGTCACAGCTAGTTGTGGATTGGATTGCCATTCTCCGAGTGTTTTAGCGTGACAGCCGCAGGGATCCCATAAAATGCAATCGTAGTCCACCTGATCGTACTTAGAAATGAGGGTCCGCTTTTGCCCACGCACCTGATCGCTCCTCGTTTGCTTTTAAGAACCGGACGAACCACAGAGCATAAGGAGAACCTCTAGCTGCTTTACAAAGTACTGGTTCCCTTTCCAGCGGGATGCTTTATCTAAACGCAATGAGAGAGGTATTCCTCAGGCCACATCGCTTCCTAGTTCCGCTGGGATCCATCGTTGGCGGCCGAAGCCGCCATTCCATAGTGAGTTCTTCGTCTGTGTCATTCTGTGCCAGATCGTCTGGCAAATAGCCGATCCAGTTTATCTCTCGAAACTATAGTCGTACAGATCGAAATCTTAAGTCAAATCACGCGACTAGACTCAGCTCTATTTTAGTGGTCATGGGTTTTGGTCCCCCCGAGCGGTGCAACCGATTAGGACCATGTAGAACATTAGTTATAAGTCTTCTTTTAAACACAATCTTCCTGCTCAGTGGTACATGGTTATCGTTATTGCTAGCCAGCCTGATAAGTAACACCACCACTGCGACCCTAATGCGCCCTTTCCACGAACACAGGGCTGTCCGATCCTATATTACGACTCCGGGAAGGGGTTCGCAAGTCGCACCCTAAACGATGTTGAAGGCTCAGGATGTACACGCACTAGTACAATACATACGTGTTCCGGCTCTTATCCTGCATCGGAAGCTCAATCATGCATCGCACCAGCGTGTTCGTGTCATCTAGGAGGGGCGCGTAGGATAAATAATTCAATTAAGATATCGTTATGCTAGTATACGCCTACCCGTCACCGGCCAACAGTGTGCAGATGGCGCCACGAGTTACTGGCCCTGATTTCTCCGCTTCTAATACCGCACACTGGGCAATACGAGCTCAAGCCAGTCTCGCAGTAACGCTCATCAGCTAACGAAAGAGTTAGAGGCTCGCTAAATCGCACTGTCGGGGTCCCTTGGGTATTTTACACTAGCGTCAGGTAGGCTAGCATGTGTCTTTCCTTCCAGGGGTATGCGGGTGCGTGGACAAATGAGCAGCATACGTATTTACTCGGCGTGCTTGGTCTCTCGTATTTCTCCTGGAGATCAAGGAAATGTTTCATGTCCAAGCGAAAAGCCGCTCTACGGAATGGATCTACGTTACTGCCTGCATAAGGAGACCGGTGTAGCCAAGGACGAAAGCGACCCTAGGTTCTAACCGTCGACTTTGGCGGAAAGGTTTCACTCAGGAAGCAGACACTGATTGACACGGTTTAGCAGAACGTTTGAGGACTAGGTCAAATTGAGTGGTTTAATATCGGCATGTCTGGCTTTAAAATTCAGTATAGTGCGCTGATCGGAGACGAATTAAAAACACGAGTTCCCAAAACCAGGCGGGCTCGCCACGTCGGCTAATCCTGGTACATTATGTGAACAATGTTCTGAAGAAAATTTGTGAAAGAAGGACGGGTCATCGCCTACTATTAGCAACAACGGTCGGCCACACCTTCCATTGTCGTGGCCACGCTCGGATTACACGGCAGAGGTGCTTGTGTTCCGACAGGCTAGCATATTATCCTAAGGCGTTACCCCAATCGTTTACCGTCGGATTTGCTATAGCCCCTGAACGCTACATGTACGAAACCATGTTATGTATGCACTAGGTCAACAATAGGACATAGCCTTGTAGTTAACACGTAGCCCGGTCGTATAAGTACAGTAGACCCTTCGCCGGCATCCTATTTATTAAGTTATT";
char str2[] = "TGCAACCCCTATCGCCATCGATTGTTTCTGCGGACGGTGTTGTCCTCATAGTTTGGGCATGTTTCCCTTGTAGGTGTGAAACCACTTAGCTTCGCGCCGTAGTCCTAAAGGAAAACCTATGGACTTTGTTTCGGGTAGCACCAGGAATCTGAACCATGTGAATGTGGACGTGGCGCGCGTACACCTTAATCTCCGGTTCATGCTAGGGATGTGGCTGCATGCTACGTTGACACACCTACACTGCTCGAAGTAAATATACGAAGCGCGCGGCCTGGCCGGAGCCGTTCCGCATCGTCACGTGTTCGTTTACTGTTAATTGGTGGCACATAAGCAATATCGTAGTCCGTCAAATTCAGCCCTGTTATCCCCGGCGTTATGTGTCAAATGGCGTAGAACTGGATTGACTGTTTGACGGTACCTGCTGATCGGTACGGTGACCGAGAATCTGTCGGGCTATGTCACTAATACTTTCCAAACGCCCCGTATCGATGCTGAACGAATCGATGCACGCTCCCGTCTTTGAAAACGCATAAACATACAAGTGGACAGATGATGGGTACGGGCCTCTAATACATCCAACACTCTACGCCCTCTTCAAGAGCTAGAAGGGCACCCTGCAGTTGGAAAGGGAATTATTTCGTAAGGCGAGCCCATACCGTCATTCATGCGGAAGAGTTAACACGATTGGAAGTAGGAATAGTTTCGAACCACGGTTACTAATCCTAATAACGGAACGCTGTCTGAAGGATGAGTGTCAGCGAGTGTAACTCGATGAGCTACCCAGTAGTCGAACTGGGCGAGACAACCCGGCGCTAATGCACTCAATCCCGAGGCCTGACGCGACATATCAGCTTAGAGTTGACGTTTGGGGTTGAATAAATCTATTGTACTAATCGGCTTCAACGTGCCCCACGGGTGGCACCTCAGGAGGGGCCCACAGCGAGGAAGTAAACTGTTATTCGTCGGCGATGGTGGTAGCTAATTATGTTCCTTGCCACTACAATAGTATCTAAGCCGTGTAATGGGAACATCCACACTTTAGTGAATCGATGCGCGGCTTCAGAATACCGTTTTGGCTACCTGTTACTAAGCCCATCGTGGTTTTCAGATATCGTGCACGTAGGGTTGCACCGCACGCATGTGGAATTAGTGGCGAAGTACGATTCCACGACCGACGTACGATTCAACTATGCGGACGTGACGAGCTTCTTTTATATGCTTCGCCCGCCGGACCGGCCTCGTGATGGGGTAGCTGCGCATAAGCTTATGACAATTAACGAGTGTGTACTCGTTTTATCATCTCACAGTTAAAGTCGGGAGAATAGGAGCCGCTACACACAATTTACCGCATCTAGACCTAACTGAGATACTGCCATAGACGACTACCCATCCCTCTGGGCCTTAGATAGCCGGATACAGTGACTTTGAAAGGTTTGTGGGGTACAGCTATGACTTGCTTAGCTGCGTGTGGGGGAAGGAACTTTTGCGTGTTAGTATGTTGACCCGTGTATTACGCATGCGGGTAGATTATGTAGGTAGAGACATCCAGGTCAAGTTCTCGACCTTCTCGTGGGAGGTGAACCAGTTCACTATAGGACCATTCCGTTCGAGCATGGCACTAAGTACGCCCTCCCCATTCTGGTAATCTTCATCCCTATCAGGGCTTGGAGTGAATGGTGAGGGTTATTCCCCAGGAACAGACTTCCTACTCACAGTCGGTCACATTGGGCTACTCCTTGGGTCTTCGGCTTGACCCGGTCTGTTGGGCCGCGATTGCGTGAGTTTCGGCCCTGCGCTGCGCTGTATAGCCCCTTCTCATCCGGGCCTCACATCTGGAAACCCCAACCTATTTAGACAGCATCATTGGCCGAAGTTGCTGGGCATGTCCACCGTGAAGTCCTCCCCGGGCGTCCCTCCTTCAAAAGACGATAAGCTCCGGCAAGCACCATTGATCAACGCAAGGATCGGTGATGTTAACAAAGATTCGGCACATTACTCTTGTTGGTGTGGTATCGCTTAACTGCGCGGCGGAGCCTTATGGCAAAACCGTTCGGGAATGATTCCGGTAGCGCTAAAGGTCCATAGCACGTACATCGCAACCTGGCGTGCGTTCAATTTGACGACCGCTTGGCGCTAAGGTGCTGGCCACGTGCTAAATTAAAGCGGCTGCACTGCTGTAAGGACGATTACGGAGTGGGCGGCCTGGGGGGAGCACTACCCCATCGACCTGTACAGGAACACTCTATATTGCTCTCAGACGAACAAATTACTAGAGTGCCGCTTTCAGCCCCCCTGTCGTCGCCGACGTCTGTAATATGGCGTTGTTGTGATTCGACTCTATTGAGGCATCAACTGATGCGTAAGGAGATCTGGAATGAATTGGCCTATGTCACTGAAACTGTCCAAACACCCAATGTCGTTAGTGAAGGTTCTGACGCATACCTCCTTCGTTGAGAACTCACAATTATACAACTGGGGACATAATCCCTACGCCCATCATCTACACGCGTCTCTGTGGCTCCAGTTCATGTATTGGGAGAGTATCCTCCACAAGATCTAGTGGTATGGTGGTATAGTAAGCTCGTACTGTGATACACGCGACAGGGGTAGGACCATCAGTAATAGGGATAGTGCGAAAGCTCACTGACCACTGCCTATAGGGGGTGCTTACTTTTAGAAAAAGTGTCAGCCAGTATAACCCCACGAGGATTCGAAAAGGTGAACCGAGCCAGACAATCCGGAGGCACGGGGCTCAAAGCCGCGACACGACGGCTCTCGGCCGGTAACAGTAACCCCGGAGTGAACACCTATGGGGCTGGATAAAACTGCCCTGGTGAGCGCCATCAGCAACCCGAATACGTGGCATTTCAGGAGGCGGCCGGAGGGGGGATGTCTTCTACTATTCGAGGCCGTTCGTTAATACTTGTTGCGTTCCTAGCCGCTATATTTGTCTCTTTGCCGACTAATGTGAACAACCACACCATAGCGATTTATCGGAGCGCCTCGGAATACGGTATGAGCAGGCGCCTCGTGAGACCATTGCGAATACCAGGTATCGTGTAAGTAGCGAAGGCCCGTACGCGAGATAAACTGCTAGGAAACCGCGTCTCTACGACCGGTGCTCGATTTAATTTCGCTGACGTGATGACATTCCAGGCAGTGCGTCTGCTGCCGGGTCCCTCTCGTGATTGGGTAGTTGGACATGCCCTTGAAAGACATAGCAAGAGCCTGCCTCTCTATTGATGTCACGGCGAATGTCGGGGAGACAGCAGCGGCTGCAGACATTACATCGGAGTAACACTAAGGTGGGATAACTCCGTAACAGACTACGCCTTTCTCTAGACCTTACTTGACCAGATACACTGTCTTTGACACGTTGATGGATTAGAGCAATCACATCCAAGACTGGCTATGCACGAAGCAACTCTTGAGTGTTAAAATCGATTGCGTGAGTTTCGGCCCTGCGTTGTCTCCTGTATTCGGGATGCGGGTACTAGATGACTGCAGGGACTCCGACGTTAAGTACATTACCCTGTCATAGGCGGCGTTCAGGATCACGTTACCGCCATATGATGCGAGCATGACATCATCTCCGCTGTGCCCACCCCAGTAGTGATTATTCCTATAACCCTTCTGAGTGTCCGGAGGCGGAAATCCGCCACGAATGAGAATGTATTTCCCCGACAATCATAATGGGGCGCTCCTAAGCTTTTCCACTTGGTTGGGCCGGCTAGGCCTCTCTGCCCGGAGTTTCGGCGCACTGCTGCCGACAGCCGGGCATTGTTTTAGGGGCGTTATTCGAGGGCACTCGGAGCTAACTTGTCGGGACCAGCCGGGGTAGTCATCGGGCTTATACAGCGAAAAGCCCAGGACCCGGCTCCACGCTATGGAACGTCTTTAGCTCCGGCAAGCAATTAAGAACAACGCAAGCATCGCGGATATAAACAGAGAAACGGCCGAATACACCTGTTCGTATCGTATCGGTAAATAGCCTCGCGGAGCCATGTGCCATACTGGTCTGCGGAGCACTCTGGTTATGCATATGGTCCACACTCGTCGCTTCCGGGTATGCGCTCTATGTGACGGTCTTTAGGCGCACTAATGCTCAGCACCATTTAAACCAGACCGACACCAGATCTGTAAGGTCCGCCACGCAGACGACAGCCCACGGAGATCACCGACCGATCTATCTGATCGGCGACCATTTGTGTGGTACTGGGGCGGAGAGGTAACTACGGTGCCGCTAACAACCCCTCTGTCGTCGCTGACGTTTGTAGTCTAGTCTCATTATGATTGTACGCTATTCAGGGATTGACTGATACCGGAAGACATCTCAGTTGAAGTGGTCTATACGACAGAGACCGTGCACCTACCAAATCTCCTTAGTGTAAGTTCAGACCAATTGGTAGTTTGTCCAGAACTCAGATTTTAACAGCAGAGGACGCATGCTCTACCTTCATGATCCACTGACGTCCCTGAGGCTGCAATACATGCAACGAGGCAGTCTCCGCGGTAAGTCCTAGTGCAATGGCGCTTTTTTACCCTCGTCCTCGAGAAGAGGGGACGCCAGTGCAGATATCTTTAATGTGGTAATTGGGAGGACTCTTGGCCCTCCGCCCTTAGGCAGTGCATACTCTTCCATAAACGGGCTGTTAGTTATGGCGTCCGAGGATTCAAAAAGGTGAGCGAACTCGGCCGATCCGGAGAGACGGGCTTCAAAGCTGCCTGACGACGGTTGCGCGTCCGTATCAAAATCCTCCTAATAAGCCCCCGTCACTGTTGGTTGAAGAGCCCAGGACGGGTTGGCCAGATGTGCGATTATATCGCTTAATGGCTCTTGGGCCGCGGTGCGTTACCTTGCAGGAATTGAGGCCGTCCGTTAATTTCCCTTGCATACATATTGCGTTTTTTTGTCTTTTTATCCGCTTACTTAGATAAGAGTGACATAGCTTCTTACCGGAGCGCCTCCGTACACAGTACGATCGCACGCCCCATGAGATCGATAGGTATACCAGGTGTCCTGTGAGCAACGAAAGCCTAAACGGGAAATACGCGGCCAAAAGTCGGTGCGAATACGAGTCGTAGCAATGTTGGTCTGGCTATGATCTACATATTTCAGGCGGTACGTCTGCTCTGGTCAGCCTCTAATGGCTCGTTAGATAGTCTAGCCGCTGGTAATCACTCGATGACCTCGGCTCCCCATTGGTGCTACGGCGATTCTTGGAGAGCCAGCTGCGATCGCTAATGTGAGGACAGTGTAATATTAGCAAGCGATAAGTCCCCAACTGGTTGTGGCCTTTTGAAAAGTGAACTTCATAACATATGCTGTCTCACGCACATGGATGGTTTGGACAAATTTGATTCAAGTCTGATCAACCTTCACACAGATCTAGAATCAAAAGCAGTGATCTCCCGGGTGCGAAATAAAAATACTAGGTAACTAGAGGGACTGCGACGTTCTAAACGTTGGTCCGTCTGAACCGCCATCCAGGATCACGTCGCCCCGAAAAAAAGATATCAGGAACTCTCCTCCTCAGCAGTCAGGTCTATGGAAACTACAGGACTAACCTTCCTGGCAACCGGGGGGTGGGAATCCGTCACATATGAGAAGGTATTTGCTCGATAATCAATACTCCAGGCATCTAACTTTTCCCACTGCCTTAAGCCGGCTTGCCCTTTCTGCCTGTAGATCCATAGGACTCGTGCCAACGCGCAGGCATAGTTCGAGGAGAAATATCCGGGGCCAAAGACAACCAGCATCTCGGGTCTTGCCCAACCCGCCTACATGCTGTTATAGCGAATCAGTGGAAACCCGGTGCCAGGCGATGGAATGTCCTTAACTCTGGCAGGAAATTAAAGGGAACGTATATACAACGCAAAGAAGCTGGAAAATTGGCGAGAGAATCTTCTTTCTGTCTATCGAAGAATGGGCATGGGGTGGCAACCGTCATGCTAGCGTGCGGGGTGCACTTGGTAACCATTTGGGACACCGGACACTCGCTGTTTTCGAAATTACCCTTTAAGCGCGGGTATTGAACCAGGCTTATGCCCAGCATCGTTGCAAGCAGACTCAAACTAGATATATTATGCCCGCCATACAGACGAAACTAGTCGGAGATTATCGAGCATACTATCACGTCGGCGACCACTAGTGAGTTACTAGAGCCGAGGGGCAACGTTGATGCCGCTAAGAACCTCTGGCTCGACGCAAGCCATAACACCCCTGTCACATCATAATCGTTTGCAATTCAGGGCTTGATCAACACTGGATTGCCTTTCTCTTAAAGTATTATGCAGGACGGGGTGCGCGTACCATGTAAACCTGTTATAACTTACCTGAGACTAGTTGGAAGTGTGGCTAGATCTTAGCTTACGTTTCTAGTCGGTCCACGTTTGGTTTTTAAGATCCAATGATCTTCAAAACGCTGCAAGATTCACAACCTGCTTTACTAAGCGCTGGGTCCTACTGCAGCGGGACTTTTTTTCTAAAGACGTTGAGAGGAGCAGTCGTCAGACCACATAGCTTTCATGTCCTGATCGGAAGGATCGTTGGCGCCCGCCTTAGACTCTGTACTGAGTTCTATAAACGAGCCATTGCATACGAGATCGGTAGATTGATAAGGGACACAGAATATCCCCGGACGCAATAGACGGACAGCTTGGTATCCTAAGCACAGTCGCGCGTCCGAACCTAGCTCTACTTTAGAGGCCCCGGATTCTGGTGCTCGTAGACCGCAGAACCGATTGGGGGGATGTACAACAATATTTGTTAGTCACCTTTGGGTCACGATCTCCCACCTTACTGGAATTTAGTCCCTGCTATAATTTGCCTTGCATATAAGTTGCGTTACTTCAGCGTCCTAACCGCACCCTTAGCACGAAGACAGATTTGTTCATTCCCATACTCCGGCGTTGGCAGGGGGTTCGCATGTCCCACGTGAAACGTTGCTAAACCCTCAGGTTTCTGAGCGACAAAAGCTTTAAACGGGAGTTCGCGCTCATAACTTGGTCCGAATGCGGGTTCTTGCATCGTTCGACTGAGTTTGTTTCATGTAGAACGGGCGCAAAGTATACTTAGTTCAATCTTCAATACCTCGTATCATTGTACACCTGCCGGTCACCACCCAACGATGTGGGGACGGCGTTGCAACTTCGAGGACCTAATCTGACCGACCTAGATTCGGCACTGTGGGCAATATGAGGTATTGGCAGACACCCAGTGCCGAACAACACCTGACCTAACGGTAAGAGAGTCTCATAATGCGTCCGGCCGCGTGCCCAGGGTATATTTGGACAGTATCGAATGGACTGAGATGAACCTTTACACCGATCCGGAAACGGGTGCGTGGATTAGCCAGGAGCAAACGAAAAATCCTGGGCTACTTGATGTCTTGTGACGTTCTTAGAGATGGACGAAATGTTTCACGACCTAGGATAAGGTCGCCCTACAAAATAGATTTGTGCTACTCTCCTCATAAGCAGTCCGGTGTATCGAAAGAACAAGACTAGCCTTGCTAGCAACCGCGGGCTGGGGGGCTAAGGTATCACTCAAGAAGCAGGCTCGGTAACATACGGTCTAGCTATCTGACTATCGCCTACGTCATATAGGGACCTATGATATCTGCGTGTCCAACCTTAGAATTCACTTCAGCGCGCAGGTTTGGGTCGAGATAAAATCACCAGTACCCAAGACCACGGGCGCTCGGCGCCTTGGCTAATCCCGGTACATGTTGTTATAAATAATCAGTAGAAAATCTGTGTTAGAGGGTCGAGTCACCATATATCAAGAACGATATTAATCGGTGGGAGTATTCAACGTGATGAAGACGCTGGGTTTACGTGGGAATGGTGCTTCTGTCCTAACAGGCTAGGGTATAATGCTGAAACCGTCCCCCAAGCGTTCAGGGTGGGGTTTGCTACGACTTCCGAGTCCAAAGTGTCCGTGTTTTTGATATATACGCTCAAGGGCGAGAATTGGACCTGGCTTACGTCTTAGTACGTAGCATGGTGACACAAGCACAGTAGATCCTGCCCGCGTTTCCTATATATTAAGTTAAATCTTATGGAATATAATAACATGTGGATGGCCAGTGGTCGGTTGTTACACGCCTACCGCAATGCTGAAAGACCCGGACTAGAGTGGCGAGATCTATGGCGTGTGACCCGTTATGCTCCATTTCGGTCAGTGGGTCACAGCTAGTTGTGGATTGGATTGCCATTCTCCGAGTGTTTTAGCGTGACAGCCGCAGGGATCCCATAAAATGCAATCGTAGTCCACCTGATCGTACTTAGAAATGAGGGTCCGCTTTTGCCCACGCACCTGATCGCTCCTCGTTTGCTTTTAAGAACCGGACGAACCACAGAGCATAAGGAGAACCTCTAGCTGCTTTACAAAGTACTGGTTCCCTTTCCAGCGGGATGCTTTATCTAAACGCAATGAGAGAGGTATTCCTCAGGCCACATCGCTTCCTAGTTCCGCTGGGATCCATCGTTGGCGGCCGAAGCCGCCATTCCATAGTGAGTTCTTCGTCTGTGTCATTCTGTGCCAGATCGTCTGGCAAATAGCCGATCCAGTTTATCTCTCGAAACTATAGTCGTACAGATCGAAATCTTAAGTCAAATCACGCGACTAGACTCAGCTCTATTTTAGTGGTTGGGTTTTGGTCCCCCCGAGCGGTGCAACCGATTAGGACCATGTAGAACATTAGTTATAAGTCTTCTTTTAAACACAATCTTCCTGCTCAGTGGTACATGGTTATCGTTATTGCTAGCCAGCCTGATAAGTAACACCACCACTGCGACCCTAATGCGCCCTTTCCACGAACACAGGGCTGTCCGATCCTATATTACGACTCCGGGAAGGGGTTCGCAAGTCGCACCCTAAACGATGTTGAAGGCTCAGGATGTACACGCACTAGTACAATACATACGTGTTCCGGCTCTTATCCTGCATCGGAAGCTCAATCATGCATCGCACCAGCGTGTTCGTGTCATCTAGGAGGGGCGCGTAGGATAAATAATTCAATTAAGATATCGTTATGCTAGTATACGCCTACCCGTCACCGGCCAACAGTGTGCAGATGGCGCCACGAGTTACTGGCCCTGATTTCTCCGCTTCTAATACCGCACACTGGGCAATACGAGCTCAAGCCAGTCTCGCAGTAACGCTCATCAGCTAACGAAAGAGTTAGAGGCTCGCTAAATCGCACTGTCGGGGTCCCTTGGGTATTTTACACTAGCGTCAGGTAGGCTAGCATGTGTCTTTCCTTCCAGGGGTATGCGGGTGCGTGGACAAATGAGCAGCATACGTATTTACTCGGCGTGCTTGGTCTCTCGTATTTCTCCTGGAGATCAAGGAAATGTTTCATGTCCAAGCGAAAAGCCGCTCTACGGAATGGATCTACGTTACTGCCTGCATAAGGAGACCGGTGTAGCCAAGGACGAAAGCGACCCTAGGTTCTAACCGTCGACTTTGGCGGAAAGGTTTCACTCAGGAAGCAGACACTGATTGACACGGTTTAGCAGAACGTTTGAGGACTAGGTCAAATTGAGTGGTTTAATATCGGCATGTCTGGCTTTAAAATTCAGTATAGTGCGCTGATCGGAGACGAATTAAAAACACGAGTTCCCAAAACCAGGCGGGCTCGCCACGTCGGCTAATCCTGGTACATTATGTGAACAATGTTCTGAAGAAAATTTGTGAAAGAAGGACGGGTCATCGCCTACTATTAGCAACAACGGTCGGCCACACCTTCCATTGTCGTGGCCACGCTCGGATTACACGGCAGAGGTGCTTGTGTTCCGACAGGCTAGCATATTATCCTAAGGCGTTACCCCAATCGTTTACCGTCGGATTTGCTATAGCCCCTGAACGCTACATGTACGAAACCATGTTATGTATGCACTAGGTCAACAATAGGACATAGCCTTGTAGTTAACACGTAGCCCGGTCGTATAAGTACAGTAGACCCTTCGCCGGCATCCTATTTATTAAGTTATT";
dist = eddist_iter(str1, str2, strlen(str1), strlen(str2));
printf("Edit distance: %d\n", dist);
}
スペルを間違えても単語の意味を表示してくれる英和辞書プログラム dictionary.c を作せよ。具体的には、ユーザーが入力した単語と完全一致している単語がなければ、辞書に登録されている単語の中から、入力された文字列との編集距離が最短の項目を探して、編集距離が3以下であれば、その定義を表示する仕組みにすること。
辞書データ: dictionary.txt
実行結果の例(1):
検索したい単語を入力してください
elephant
elephant は 象 です
実行結果の例(2):
検索したい単語を入力してください
elephnat
elephnat という単語は辞書に登録されていません
elephant のことでしょうか?
elephant は 象 です
実行結果の例(3):
検索したい単語を入力してください
racoon
racoon という単語は辞書に登録されていません
発展課題
dictionary.c で用いた、ユーザー入力にマッチする辞書項目を探す方法の弱点は何ですか?改善する方法を考えて実装すること。